题目内容
如图所示,有一倾角为![]() 的光滑绝缘细杆,其长度为L,在细杆底端固定一带正电小球B。现将一质量为m,电荷量为q的带正电小球A套在细杆上,从最高点由静止释放,小球在到达细杆中点C时达到最大速度Vm。若重力加速度为g,静电力常量为k。求:
的光滑绝缘细杆,其长度为L,在细杆底端固定一带正电小球B。现将一质量为m,电荷量为q的带正电小球A套在细杆上,从最高点由静止释放,小球在到达细杆中点C时达到最大速度Vm。若重力加速度为g,静电力常量为k。求:
(1)小球B所带电荷量为多大?
(2)小球A在最高点的加速度为多少?
(3)从A到C的过程中库仑力做的功是多少?

(1)![]() (2)a=
(2)a=![]() g sinq(3)W库=
g sinq(3)W库=![]() mVm2-
mVm2-![]() mgLsinq
mgLsinq
解析:
(1)因为小球在C点达到最大速度
所以小球在C处所受合力为零,设B带电量为QB
即F库=mg·sinq ① ……………………(1分)
由库仑定律得F库=k![]() ②……………………(1分)
②……………………(1分)
由①②得:QB=![]() ……………………(2分)
……………………(2分)
(2)在最高点对小球作受力分析,由牛顿第二定律得:
F合=mgsinq-F'库=ma ③……………………(1分)
F'库=k![]() =
=![]() mgsinq ④ ……………………(1分)
mgsinq ④ ……………………(1分)
由③④得:a=![]() g sinq…………………………(2分)
g sinq…………………………(2分)
(3)从A到C由动能定理得:
mg·![]() ·sinq+W库=
·sinq+W库=![]() mVm2-0
mVm2-0
\W库=![]() mVm2-
mVm2-![]() mgLsinq ……………………(6分)
mgLsinq ……………………(6分)

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 (2005?和平区一模)如图所示,有一倾角为30°的光滑斜面,斜面长l为10m,一小球从斜面顶端以10m/s的速度沿水平方向抛出,求:
(2005?和平区一模)如图所示,有一倾角为30°的光滑斜面,斜面长l为10m,一小球从斜面顶端以10m/s的速度沿水平方向抛出,求: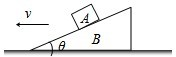 如图所示,有一倾角为θ的斜面体 B静置在水平地面上,物体A放在斜面上且与B保持相对静止.现对斜面体B施加向左的水平推力,使物体A和斜面体B一起向左做加速运动,加速度从零开始逐渐增大,直到A和B开始发生相对运动,则关于A物体受到B物体的支持力FN和摩擦力Ff,下列说法正确的是( )
如图所示,有一倾角为θ的斜面体 B静置在水平地面上,物体A放在斜面上且与B保持相对静止.现对斜面体B施加向左的水平推力,使物体A和斜面体B一起向左做加速运动,加速度从零开始逐渐增大,直到A和B开始发生相对运动,则关于A物体受到B物体的支持力FN和摩擦力Ff,下列说法正确的是( ) 如图所示,有一倾角为θ的斜面体 B静置在水平地面上,物体A放在斜面上且与B保持相对静止.现对斜面体B施加向左的水平推力,使物体A和斜面体B一起向左做加速运动,加速度从零开始逐渐增大,直到A和B开始发生相对运动,则关于A物体受到B物体的支持力FN和摩擦力Ff,下列说法正确的是( )
如图所示,有一倾角为θ的斜面体 B静置在水平地面上,物体A放在斜面上且与B保持相对静止.现对斜面体B施加向左的水平推力,使物体A和斜面体B一起向左做加速运动,加速度从零开始逐渐增大,直到A和B开始发生相对运动,则关于A物体受到B物体的支持力FN和摩擦力Ff,下列说法正确的是( ) 如图所示,有一倾角为30°的光滑斜面,匀强磁场垂直斜面,匀强电场沿斜面向上并垂直斜面底边.一质量为m、带电荷量为q的小球,以速度v在斜面上做半径为R匀速圆周运动.则( )
如图所示,有一倾角为30°的光滑斜面,匀强磁场垂直斜面,匀强电场沿斜面向上并垂直斜面底边.一质量为m、带电荷量为q的小球,以速度v在斜面上做半径为R匀速圆周运动.则( ) (2013?湖北模拟)如图所示,有一倾角为θ=37°的斜面AB固定在水平面MN上.现有两个可视为质点的小球P和Q,同时由静止开始释放,小球P从斜面最高点A点沿斜面运动到斜面最低点B点,小球P与斜面间的摩擦因数
(2013?湖北模拟)如图所示,有一倾角为θ=37°的斜面AB固定在水平面MN上.现有两个可视为质点的小球P和Q,同时由静止开始释放,小球P从斜面最高点A点沿斜面运动到斜面最低点B点,小球P与斜面间的摩擦因数