题目内容
如图所示、传送带的水平部分AB长为=5米,以V0=4m/s的速度向右匀速运动,水平台面与传送带平滑连接与B点,BC长S=1米,台面右边有高为h=0.5m的光滑曲面CD。一质量m=1kg的工件(可以视为质点),从A点无初速度释放,工件与传送带及台面间的动摩擦因数均为0.2,g=10米每二次方秒,求

(1)工件运动到B点时的速度大小
(2)通过计算说明,工件能否通过D点到达上平台DE上。
略
解析:
(1)工件刚放上时,做初速度为零的匀加速直线运动,
由牛顿第二定律得:μ mg=ma ………(2分)
解得:a=2m/s2
当两者速度相等时,![]()
工件对地的位移为:![]() ………(2分)
………(2分)
因此,工件到达B点的速度为:![]() ………(3分)
………(3分)
(2)设工件沿曲面CD上升的最大高度为h′,
由动能定理得:![]() ………(4分)
………(4分)
解得 h′=0.6m>h
所以,工件能够通过D点到达平台DE上。………(3分)

练习册系列答案
相关题目
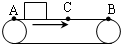 水平传送带装置如图所示,皮带的速度保持不变,物体被轻轻地放在皮带上A端.开始时物体在皮带上滑动,当它运动到C点时就不再相对滑动,而是随传送带一起匀速运动,直至传送到B端,在传送过程中,物体受到的摩擦力( )
水平传送带装置如图所示,皮带的速度保持不变,物体被轻轻地放在皮带上A端.开始时物体在皮带上滑动,当它运动到C点时就不再相对滑动,而是随传送带一起匀速运动,直至传送到B端,在传送过程中,物体受到的摩擦力( )| A、在AC段为水平向左的滑动摩擦力 | B、在AC段为水平向右的滑动摩擦力 | C、在CB段水不受摩擦力 | D、在CB段受水平向右的静摩擦力 |
 如图所示为一皮带传送装置,皮带保持匀速率运动,货物由静止放到传送带上,被传送带向下传送,其运动的v-t图象如图乙所示.
如图所示为一皮带传送装置,皮带保持匀速率运动,货物由静止放到传送带上,被传送带向下传送,其运动的v-t图象如图乙所示. 如图所示,质量为2m,长为1的木块置于光滑水平台面上,质量为m的子弹以初速度v0水平向右射向木块,穿出木块时的速度为
如图所示,质量为2m,长为1的木块置于光滑水平台面上,质量为m的子弹以初速度v0水平向右射向木块,穿出木块时的速度为 如图所示,质量为m的滑块,放在光滑的水平平台上,平台右端B与水平传送带相接,传送带的运行速度为v?,长为L,今将滑块缓慢向左压缩固定在平台上的轻弹簧,到达某处时突然释放,当滑块滑到传送带右端C时,恰好与传送带速度相同.滑块与传送带间的动摩擦因数为μ.
如图所示,质量为m的滑块,放在光滑的水平平台上,平台右端B与水平传送带相接,传送带的运行速度为v?,长为L,今将滑块缓慢向左压缩固定在平台上的轻弹簧,到达某处时突然释放,当滑块滑到传送带右端C时,恰好与传送带速度相同.滑块与传送带间的动摩擦因数为μ.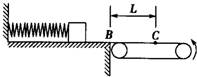 如图所示,质量为m=1kg的滑块,放在光滑的水平平台上,平台的右端B与足够长的水平传送带相接,皮带轮的半径为R=o.5m,且以角速度ω=12rad/s逆时针转动(传送带不打滑),先将滑块缓慢向左压缩固定在平台上的轻弹簧,然后突然释放,当滑块滑到传送带上距B端L=15m的C点时,与传送带速度大小相等,滑块与传送带之间的动摩擦因数μ=0.15.(g=10m/s2)求:
如图所示,质量为m=1kg的滑块,放在光滑的水平平台上,平台的右端B与足够长的水平传送带相接,皮带轮的半径为R=o.5m,且以角速度ω=12rad/s逆时针转动(传送带不打滑),先将滑块缓慢向左压缩固定在平台上的轻弹簧,然后突然释放,当滑块滑到传送带上距B端L=15m的C点时,与传送带速度大小相等,滑块与传送带之间的动摩擦因数μ=0.15.(g=10m/s2)求: