题目内容
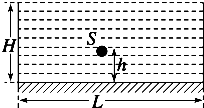在厚度为d、折射率为n的大玻璃板的下表面，有一个半径为r的圆形发光面．为了从玻璃板的上方看不见圆形发光面，可在玻璃板的上表面贴一块圆形纸片，所贴纸片的最小半径为多大？分析：作出光路图，S点为圆形发光面边缘上一点．由该点发出的光线能射出玻璃板的范围由临界光线SA确定，当入射角大于临界角C时，光线就不能射出玻璃板了．根据折射定律和几何知识结合进行求解．
解答：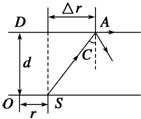
解：根据题述，光路如图所示，图中S点为圆形发光面边缘上一点，
由该点发出的光线能射出玻璃板的范围由临界光线SA确定，当入射角大于临界角C时，光线就不能射出玻璃板了．
图中△r=dtanC=d
，而sinC=
，
则cosC=
，所以△r=
．故所贴纸片的最小半径R=r+△r=r+
．
答：所贴纸片的最小半径为r+
．
解：根据题述，光路如图所示，图中S点为圆形发光面边缘上一点，由该点发出的光线能射出玻璃板的范围由临界光线SA确定，当入射角大于临界角C时，光线就不能射出玻璃板了．
图中△r=dtanC=d
| sinC |
| cosC |
| 1 |
| n |
则cosC=
| ||
| n |
| d | ||
|
| d | ||
|
答：所贴纸片的最小半径为r+
| d | ||
|
点评：本题关键要理解看不到圆形发光面的原因是由于发生了全反射，再作出光路图，运用折射定律和几何知识结合进行求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目