题目内容
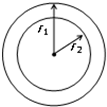（2010?湖南模拟）如图，火星和地球绕太阳的运动可以近似看作为在同一平面内的同方向的匀速圆周运动，已知火星轨道半径r1=2.3×1011m，地球轨道半径为r2=1.5×1011m，根据你所掌握的物理和天文知识，估算火星与地球相邻两次相距最近的最短时间间隔约为（ ）分析：根据万有引力提供向心力，列式可得周期的表达式，求得地球和火星的周期之比，这样可以解出火星的周期．两星转过的角度之差△θ=2π时，火星与地球相邻再次相距最近，从而求出时间．
解答：解：设行星质量为m，太阳质量为M，行星与太阳的距离为r，火星的周期为T1，地球的周期为T2．
行星绕太阳做近似匀速圆周运动，万有引力提供向心力，则根据牛顿第二定律有
G
=m
r
则得 T2=
地球的周期为T2=1年，则有(
)2=(
)3
火星的周期为T1=1.8年
设经时间t两星又一次距离最近，
根据θ=ωt
则两星转过的角度之差
△θ=（
-
）t=2π
得t=2.3年≈2年．
故选B
行星绕太阳做近似匀速圆周运动，万有引力提供向心力，则根据牛顿第二定律有
G
| Mm |
| r2 |
| 4π2 |
| T2 |
则得 T2=
| 4π2r3 |
| GM |
地球的周期为T2=1年，则有(
| T1 |
| T2 |
| r1 |
| r2 |
火星的周期为T1=1.8年
设经时间t两星又一次距离最近，
根据θ=ωt
则两星转过的角度之差
△θ=（
| 2π |
| T2 |
| 2π |
| T1 |
得t=2.3年≈2年．
故选B
点评：本题也可运用开普勒周期定律求解火星的运动周期．这种方法，很好理解，关键确定相距最近的条件．
练习册系列答案
发散思维新课堂系列答案
相关题目
（2010?湖南模拟）利用图中所示的装置，做“测定重力加速度”的实验中，得到了几条较为理想的纸带．已知每条纸带上每5个点取一个计数点，即两计数点之间的时间间隔为O.1s，依打点先后编为0，1，2，3，4，…．由于不小心，纸带都被撕断了，如图所示，根据给出的A、B、C、D四段纸带回答：
（2010?湖南模拟）如图所示，一高度为h的光滑水平面与一倾角为θ的斜面连接，一小球以速度v从平面的右端P点向右水平抛出．则小球在空中运动的时间（ ）
（2010?湖南模拟）如图所示，MN是由一个正点电荷Q产生的电场中的一条电场线，一个带正电的粒子+q飞入电场后，在电场力的作用下沿一条曲线运动，先后通过a、b两点，不计粒子的重力，则（ ）
（2010?湖南模拟）如图所示，小车内有一个光滑的斜面，当小车在水平轨道上做匀变速直线运动时，小物块A恰好能与斜面保持相对静止．在小车运动过程中的某时刻，突然使小车停止，则物体A的运动可能（ ）
（2010?湖南模拟）美国物理学家劳伦斯于1932年发明的回旋加速器，应用带电粒子在磁场中做圆周运动的特点，能使粒子在较小的空间范围内经过电场的多次加速获得较大的能量，克服了多级直线加速器的缺点，使人类在获得较高能量带电粒子方面前进了一步．下图为一种改进后的回旋加速器示意图，其中盒缝间的加速电场场强大小恒定，且被限制在A板和C板间，如图所示．带电粒子从P0处以速度V0沿电场线方向射入加速电场，经加速后再进入D型盒中的匀强磁场做匀速圆周运动．对于这种改进后的回旋加速器，下列说法正确的是（ ）