题目内容
如图所示,小球A用不可伸长的细绳悬于O点,在O点的正下方有一固定的钉子B,OB=d,初始时小球A与O同水平面无初速度释放,绳长为L,为使小球能绕B点做完整的圆周运动,则d的取值范围是 。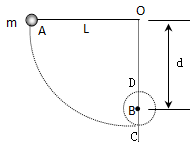
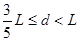
解析试题分析:球能绕B点做圆周运动,在D点根据向心力公式有: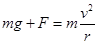
当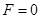 时,速度取最小值;所以
时,速度取最小值;所以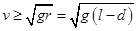
对小球从最高点运动到D点的过程中运用动能定理得: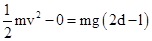 解得:
解得: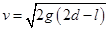 所以
所以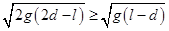 ,解得:
,解得: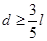 由题意得
由题意得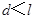
所以有: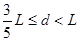
考点:向心力;牛顿第二定律.
点评:关键是把握为使球能绕B点做圆周运动,在D点的速度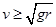 ,根据动能定理列式即可求解.
,根据动能定理列式即可求解.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 如图所示,小球C用两根长度相等、不可伸长的细线系在竖直杆上,它们随竖直杆转动,在转动角速度变化时,下列关于细线上的力的叙述不正确的是( )
如图所示,小球C用两根长度相等、不可伸长的细线系在竖直杆上,它们随竖直杆转动,在转动角速度变化时,下列关于细线上的力的叙述不正确的是( ) 如图所示,小球A和B带电荷量均为+q,质量分别为m和2m,用不计质量的竖直细绳连接,在竖直向上的匀强电场中以速度v0匀速上升,某时刻细绳突然断开.小球A和B之间的相互作用力忽略不计.求:
如图所示,小球A和B带电荷量均为+q,质量分别为m和2m,用不计质量的竖直细绳连接,在竖直向上的匀强电场中以速度v0匀速上升,某时刻细绳突然断开.小球A和B之间的相互作用力忽略不计.求:


