��Ŀ����
 ��2013?����ģ�⣩��ͼ��ʾ�����������Ⱦ�Ϊd��������������͢��ڷֱ��з���ֱ��ֽ��������������ǿ�ų�������Ϊ�ų��߽磬������ʾ�ϰ����������дų��ĴŸ�Ӧǿ�ȴ�СΪB��������дų��ĴŸ�Ӧǿ�ȴ�Сδ֪������Ϊm��������Ϊ+q�����ӣ��ӿ�O1�Դ�С��ͬ��������ͼʾ��aa��н�a=30��ķ������ų��������������Բ��ƣ�
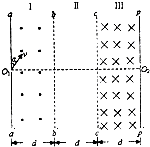
��2013?����ģ�⣩��ͼ��ʾ�����������Ⱦ�Ϊd��������������͢��ڷֱ��з���ֱ��ֽ��������������ǿ�ų�������Ϊ�ų��߽磬������ʾ�ϰ����������дų��ĴŸ�Ӧǿ�ȴ�СΪB��������дų��ĴŸ�Ӧǿ�ȴ�Сδ֪������Ϊm��������Ϊ+q�����ӣ��ӿ�O1�Դ�С��ͬ��������ͼʾ��aa��н�a=30��ķ������ų��������������Բ��ƣ���1������������������˶�ʱǡ�ò��ӱ߽�bb'������������ڸ������ڵ��˶�ʱ�䣻
��2�������Ӿ�������˶���ǡ�ô�ֱ�߽�bb'��������������Ӵӿ�O1�����ٶ�v�Ĵ�С��
��3�������������O1O2�Ϸ�����ֱ���µ���ǿ�糡��O1O2�·��ԳƼ���ֱ���ϵ���ǿ�糡����ǿ��С��ȣ�ʹ�ڣ�2�����е�����ÿ�ξ���ֱ������bb'��cc'���ܻص�O1�㣬�����Ӵ�O1�������ص�O1�˶�����ʱ�估���ӵ糡ǿ�ȵĴ�С��
��������1�����ӽ���ų�������������������������Բ���˶���ǡ�ò��ӱ߽�bb'���ʱ�켣ǡ����߽�bb'���У������켣�����ݼ���֪ʶ����켣���Ե�Բ�ĽǦȣ���t=
T���ʱ�䣮
��2�����Ӿ�������˶���ǡ�ô�ֱ�߽�bb'���������ʱ�������켣����ϼ��ι�ϵ������ӵĹ켣�뾶������ţ�ٵڶ�����������Ӵӿ�O1�����ٶ�v�Ĵ�С��
��3��ʹ�ڣ�2�������ٶ�Ϊ�Ե�����ÿ�ξ���ֱ����I��������ı߽��沢�ܻص�O1�㣬����Ҫ�������˶��Ĺ켣ͼ�����������ڵ糡������ƽ���˶�������˶�������������糡ǿ�ȵĴ�С������ų�������Բ���˶����ڴų����˶�180����ų������ݰ뾶�Ĵ�С��ϵ����Ÿ�Ӧǿ�ȵĴ�С���ֱ���������ڵ糡�кʹų����˶���ʱ�䣬�Ӷ������ʱ�䣮
| �� |
| 2�� |
��2�����Ӿ�������˶���ǡ�ô�ֱ�߽�bb'���������ʱ�������켣����ϼ��ι�ϵ������ӵĹ켣�뾶������ţ�ٵڶ�����������Ӵӿ�O1�����ٶ�v�Ĵ�С��
��3��ʹ�ڣ�2�������ٶ�Ϊ�Ե�����ÿ�ξ���ֱ����I��������ı߽��沢�ܻص�O1�㣬����Ҫ�������˶��Ĺ켣ͼ�����������ڵ糡������ƽ���˶�������˶�������������糡ǿ�ȵĴ�С������ų�������Բ���˶����ڴų����˶�180����ų������ݰ뾶�Ĵ�С��ϵ����Ÿ�Ӧǿ�ȵĴ�С���ֱ���������ڵ糡�кʹų����˶���ʱ�䣬�Ӷ������ʱ�䣮
��� �⣺��1������ǡ�ò��ӱ߽�bb��������켣����ͼ��ʾ
�⣺��1������ǡ�ò��ӱ߽�bb��������켣����ͼ��ʾ
t=
T1 ��
T1=
��
�ɢ١���ʽ��ã�t=
��2����ֱ�߽�bb'����Ĺ켣��ͼ��ʾ��ת����Բ�Ľǵã���=60��
�ɼ��ι�ϵ��֪��d=Rsin60��
�ã�R=
d ��
��qvB=m
�ã�v=
��
�Ѣ�ʽ���ˢܵã�v=
��3�����������R��=
�����ܷ��������
�� B��=2B
t��=
=
t��=
+
=
�� t=t��+t��=
+
�����������O1O2�Ϸ�����ֱ���µ���ǿ�糡ˮƽΪλ��Ϊx���˶�ʱ��Ϊt���ܴ�ֱ�߽�����������Ӧ���㣺
=
at2=
t2 ��
x=vt ��
��2n+1����2x=d ��n=0��1��2��3���� ��
�ɢۢݢޢ�ʽ�ã�E=
��n=0��1��2��3����
������ʱ��tҲ���ã�
t=
��
=
=
��
�ɢۢݢ�ʽ�ã�E=
��n=0��1��2��3����
�𣺣�1�������ڸ������ڵ��˶�ʱ��Ϊ
����2�����Ӵӿ�O1�����ٶ�v�Ĵ�СΪ
��
��3�����Ӵ�O1�������ص�O1�˶�����ʱ��Ϊ
�����ӵ糡ǿ�ȵĴ�СΪ
��n=0��1��2��3������
 �⣺��1������ǡ�ò��ӱ߽�bb��������켣����ͼ��ʾ
�⣺��1������ǡ�ò��ӱ߽�bb��������켣����ͼ��ʾt=
| 5 |
| 6 |
T1=
| 2��m |
| qB |
�ɢ١���ʽ��ã�t=
| 5��m |
| 3qB |
��2����ֱ�߽�bb'����Ĺ켣��ͼ��ʾ��ת����Բ�Ľǵã���=60��
�ɼ��ι�ϵ��֪��d=Rsin60��
�ã�R=
2
| ||
| 3 |
��qvB=m
| v2 |
| R |
| RqB |
| m |
�Ѣ�ʽ���ˢܵã�v=
2
| ||
| 3m |
��3�����������R��=
| R |
| 2 |
�� B��=2B
t��=
| 2d |
| v |
| ||
| Bq |
t��=
| T1 |
| 3 |
| T2 |
| 2 |
| 7m�� |
| 6Bq |
�� t=t��+t��=
| ||
| Bq |
| 7m�� |
| 6Bq |
�����������O1O2�Ϸ�����ֱ���µ���ǿ�糡ˮƽΪλ��Ϊx���˶�ʱ��Ϊt���ܴ�ֱ�߽�����������Ӧ���㣺
| R |
| 2 |
| 1 |
| 2 |
| Eq |
| 2m |
x=vt ��
��2n+1����2x=d ��n=0��1��2��3���� ��
�ɢۢݢޢ�ʽ�ã�E=
32
| ||
| 9m |
������ʱ��tҲ���ã�
t=
| 1 |
| 2 |
| t�� |
| 2(2n+1) |
| ||||
| 4(2n+1) |
| ||
| 4(2n+1)qB |
�ɢۢݢ�ʽ�ã�E=
32
| ||
| 9m |
�𣺣�1�������ڸ������ڵ��˶�ʱ��Ϊ
| 5��m |
| 3qB |
2
| ||
| 3m |
��3�����Ӵ�O1�������ص�O1�˶�����ʱ��Ϊ
| ||
| 4(2n+1)qB |
32
| ||
| 9m |
������������������ǿ�ų��е��˶����������е��ص㣬Ҳ�Ǹ߿��ıؿ������ݣ����ӵ��˶����̵ķ����ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
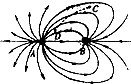 ��2013?����ģ�⣩��ͼ��ʾΪA��B�������γɵĵ糡�߷ֲ�ͼ��һ���������ӽ��ڵ糡�������´�C���˶���D�㣬�켣��ͼ������ʾ��������˵����ȷ���ǣ�������
��2013?����ģ�⣩��ͼ��ʾΪA��B�������γɵĵ糡�߷ֲ�ͼ��һ���������ӽ��ڵ糡�������´�C���˶���D�㣬�켣��ͼ������ʾ��������˵����ȷ���ǣ������� ��2013?����ģ�⣩ͼ����ijȼ��¯���װ�õ�ԭ��ͼ��ת������ֱ����ѹת��Ϊͼ����ʾ�����ҽ����ѹ��������һ�����ѹ����ԭ��Ȧ�ϣ���ѹ��ԭ������Ȧ�������ֱ�Ϊn1��n2��������ѹ��Ϊ������������ѹ������Ȧ��ѹ��˲ʱֵ����5000Vʱ���ͻ��ڸ���ͽ�����������������ȼ���壮�����ж���ȷ���ǣ�������
��2013?����ģ�⣩ͼ����ijȼ��¯���װ�õ�ԭ��ͼ��ת������ֱ����ѹת��Ϊͼ����ʾ�����ҽ����ѹ��������һ�����ѹ����ԭ��Ȧ�ϣ���ѹ��ԭ������Ȧ�������ֱ�Ϊn1��n2��������ѹ��Ϊ������������ѹ������Ȧ��ѹ��˲ʱֵ����5000Vʱ���ͻ��ڸ���ͽ�����������������ȼ���壮�����ж���ȷ���ǣ������� ��2013?����ģ�⣩��ͼ��ʾ��һ��г�Შ���ٶ�v��x����������t=0ʱ����������ԭ�㣬���ʵ�����ƽ��λ�����ٶ�v0��������֪�ʵ�����ΪA����Ƶ��Ϊ
��2013?����ģ�⣩��ͼ��ʾ��һ��г�Შ���ٶ�v��x����������t=0ʱ����������ԭ�㣬���ʵ�����ƽ��λ�����ٶ�v0��������֪�ʵ�����ΪA����Ƶ��Ϊ