题目内容
 金属杆在竖直面内构成足够长平行轨道,杆间接一阻值为R的电阻,一个质量为m的、阻值为r的长度刚好是轨道宽L的金属棒与轨道间的摩擦力恒为f,金属棒始终紧靠轨道运动.此空间存在如图所示的水平匀强磁场(×场),磁感应强度为B,当金属棒由静止下滑h时已经匀速,则此过程中整个回路产生的焦耳热为
金属杆在竖直面内构成足够长平行轨道,杆间接一阻值为R的电阻,一个质量为m的、阻值为r的长度刚好是轨道宽L的金属棒与轨道间的摩擦力恒为f,金属棒始终紧靠轨道运动.此空间存在如图所示的水平匀强磁场(×场),磁感应强度为B,当金属棒由静止下滑h时已经匀速,则此过程中整个回路产生的焦耳热为mgh-fh-
| m(mg-f)2(R+r)2 |
| 2B4L4 |
mgh-fh-
.| m(mg-f)2(R+r)2 |
| 2B4L4 |
分析:匀速运动时,受重力、摩擦力和向上的安培力,根据平衡条件列式求解安培力;根据安培力公式求解电流;再根据闭合电路欧姆定律求解电动势;根据且切割公式求解速度;最后根据功能关系列式求解焦耳热.
解答:解:匀速运动时,受重力、摩擦力和向上的安培力,根据平衡条件,有:
mg-f-FA=0
根据安培力公式,有:FA=BIL;
根据闭合电路欧姆定律,有:I=
;
根据切割公式,有:E=BLv;
根据功能关系,有:mgh=
mv2+Q+fh;
联立以上各式解得:Q=mgh-fh-
;
故答案为:mgh-fh-
.
mg-f-FA=0
根据安培力公式,有:FA=BIL;
根据闭合电路欧姆定律,有:I=
| E |
| r+R |
根据切割公式,有:E=BLv;
根据功能关系,有:mgh=
| 1 |
| 2 |
联立以上各式解得:Q=mgh-fh-
| m(mg-f)2(R+r)2 |
| 2B4L4 |
故答案为:mgh-fh-
| m(mg-f)2(R+r)2 |
| 2B4L4 |
点评:本题关键明确回路中的能量转化情况,根据平衡条件、闭合电路欧姆定律、切割公式、安培力公式、功能关系列式后联立求解,不难.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 如图,有光滑细杆构成的矩形框架ABCD位于竖直面内,其中AC竖直,E是CD边上的一点,在细杆AB、AC、AD间每相邻的两细杆之间的夹角均为30°.现让一光滑金属小环(图中未画出)从A点分别沿细杆AB、AC、AE、AD无初速地滑到B、C、E、D四点,经历的时间分别为t1、t2、t3、t4,则( )
如图,有光滑细杆构成的矩形框架ABCD位于竖直面内,其中AC竖直,E是CD边上的一点,在细杆AB、AC、AD间每相邻的两细杆之间的夹角均为30°.现让一光滑金属小环(图中未画出)从A点分别沿细杆AB、AC、AE、AD无初速地滑到B、C、E、D四点,经历的时间分别为t1、t2、t3、t4,则( )| A、t4<t3<t1<t2 | B、t3<t1=t2=t4 | C、t4<t3<t2=t1 | D、t3>t1=t2=t4 |
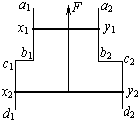 (2004?江西)图中a1b1c1d1和a2b2c2d2为在同一竖直面内的金属导轨,处在磁感应强度为B的匀强磁场中,磁场方向垂直导轨所在的平面(纸面)向里.导轨的a1b1段与a2b2段是竖直的,距离为l1;c1d1段与c2d2段也是竖直的,距离为l2.x1y1与x2y2为两根用不可伸长的绝缘轻线相连的金属细杆,质量分别为m1和m2,它们都垂直于导轨并与导轨保持光滑接触.两杆与导轨构成的回路的总电阻为R.F为作用于金属杆x1y1上的竖直向上的恒力.已知两杆运动到图示位置时,已匀速向上运动,求此时作用于两杆的重力的功率的大小和回路电阻上的热功率.
(2004?江西)图中a1b1c1d1和a2b2c2d2为在同一竖直面内的金属导轨,处在磁感应强度为B的匀强磁场中,磁场方向垂直导轨所在的平面(纸面)向里.导轨的a1b1段与a2b2段是竖直的,距离为l1;c1d1段与c2d2段也是竖直的,距离为l2.x1y1与x2y2为两根用不可伸长的绝缘轻线相连的金属细杆,质量分别为m1和m2,它们都垂直于导轨并与导轨保持光滑接触.两杆与导轨构成的回路的总电阻为R.F为作用于金属杆x1y1上的竖直向上的恒力.已知两杆运动到图示位置时,已匀速向上运动,求此时作用于两杆的重力的功率的大小和回路电阻上的热功率.
