题目内容
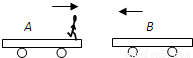
如图所示,光滑水平面上A、B两小车质量都是M,A车头站立一质量为m的人,两车在同一直线上相向运动.为避免两车相撞,人从A车跃到B车上,最终A车停止运动,B车获得反向速度v,试求:(1)两小车和人组成的系统的初动量大小;
(2)为避免两车相撞,且要求人跳跃速度尽量小,则人跳上B车后,A车的速度多大?
【答案】分析:(1)整个系统动量守恒,据此列方程可正确解答.
(2)三者最后速度相同时人跳跃速度最小,由此列动量守恒方程即可正确解答本题.
解答:解:(1)由动量守恒定律可知,系统的初动量大小:
P=(M+m)v
故两小车和人组成的系统的初动量大小为:P=(M+m)v.
(2)为避免两车恰好不会发生碰撞,最终两车和人具有相同速度(设为v),则:
(M+m)v=(2M+m)v
解得: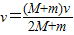
故人跳上B车后,A车的速度: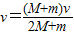 .
.
点评:应用动量守恒解题的关键是正确选择研究对象和选择两个的状态,动量守恒观点是常用的方法,注意平时不断加强应用.
(2)三者最后速度相同时人跳跃速度最小,由此列动量守恒方程即可正确解答本题.
解答:解:(1)由动量守恒定律可知,系统的初动量大小:
P=(M+m)v
故两小车和人组成的系统的初动量大小为:P=(M+m)v.
(2)为避免两车恰好不会发生碰撞,最终两车和人具有相同速度(设为v),则:
(M+m)v=(2M+m)v
解得:
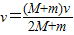
故人跳上B车后,A车的速度:
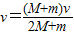 .
.点评:应用动量守恒解题的关键是正确选择研究对象和选择两个的状态,动量守恒观点是常用的方法,注意平时不断加强应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求:
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求: 如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
 (2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求:
(2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求: 如图所示,光滑水平面内,一根细绳一端固定,另一端系一小球,现让小球在水平面内做匀速圆周运动,则( )
如图所示,光滑水平面内,一根细绳一端固定,另一端系一小球,现让小球在水平面内做匀速圆周运动,则( )