题目内容
一位质量为60kg的滑雪运动员,从高为10m的斜坡上自由滑下.如果滑雪板与斜坡的动摩擦因数为
,斜坡倾角为30°.(1)运动员滑至坡底的过程中,求各个力所做的功以及坡底处运动员的速率.(取g=10m/s2)
(2)如果从坡底给运动员一个10m/s的初速度,运动员能否滑到坡顶,如果不能,能在斜坡上滑行多高?
| ||
| 6 |
(2)如果从坡底给运动员一个10m/s的初速度,运动员能否滑到坡顶,如果不能,能在斜坡上滑行多高?
分析:(1)滑雪运动员在斜坡上滑下时,受重力、支持力和摩擦力,根据功的公式分别求出各个力所做的功,根据动能定理求出运动员到达坡底的速率.
(2)根据动能定理判断运动员能上滑的距离,从而判断是否能滑动坡顶.
(2)根据动能定理判断运动员能上滑的距离,从而判断是否能滑动坡顶.
解答:解:(1)在下滑的过程中,支持力方向与速度方向垂直,不做功,所以WN=0.
WG=mgh=600×10J=6000J.
Wf=-μmgscos30°=-3000J
根据动能定理得,WG+Wf=
mv2-0
解得v=10m/s.
故支持力做功为0,重力做功为6000J,摩擦力做功为-3000J.运动员到达坡底的速度为10m/s.
(2)根据动能定理得:-mgs′sin30°-μmgs′cos30°=0-
mv02
解得:s′≈6.6m
则h′=3.3m<10m,不能到达坡顶.能在斜坡上滑行3.3m高.
故运动员不能到达坡顶,能在斜坡上滑行3.3m高.
WG=mgh=600×10J=6000J.
Wf=-μmgscos30°=-3000J
根据动能定理得,WG+Wf=
| 1 |
| 2 |
解得v=10m/s.
故支持力做功为0,重力做功为6000J,摩擦力做功为-3000J.运动员到达坡底的速度为10m/s.
(2)根据动能定理得:-mgs′sin30°-μmgs′cos30°=0-
| 1 |
| 2 |
解得:s′≈6.6m
则h′=3.3m<10m,不能到达坡顶.能在斜坡上滑行3.3m高.
故运动员不能到达坡顶,能在斜坡上滑行3.3m高.
点评:解决本题的关键掌握功的求法,以及掌握动能定理的基本运用.

练习册系列答案
相关题目
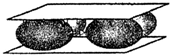 一位质量为60kg的同学为了表演“轻功”,他用打气筒给4只相同的气球充以相等质量的空气(可视为理想气体),然后将这4只气球以相同的方式放在水平放置的木板上,在气球的上方设置一轻质塑料板,如图所示.在这位同学慢慢站上轻质塑料板中间位置的过程中,球内气体温度可视为不变.则下列说法错误的是( )
一位质量为60kg的同学为了表演“轻功”,他用打气筒给4只相同的气球充以相等质量的空气(可视为理想气体),然后将这4只气球以相同的方式放在水平放置的木板上,在气球的上方设置一轻质塑料板,如图所示.在这位同学慢慢站上轻质塑料板中间位置的过程中,球内气体温度可视为不变.则下列说法错误的是( )| A、气体压强是由于气体分子之间的斥力而产生的 | B、气体压强是由于大量气体分子碰撞器壁而产生的 | C、球内气体体积变小 | D、球内气体内能不变 |

 某公园计划修建大型游乐设施“翻滚过山车”,设计轨道总长为842m,每车可载28人.游乐过程中过山车将绕半径为5.5m的大圆环回旋,如图所示.若不考虑一切阻力,取g=10m/s2,求:
某公园计划修建大型游乐设施“翻滚过山车”,设计轨道总长为842m,每车可载28人.游乐过程中过山车将绕半径为5.5m的大圆环回旋,如图所示.若不考虑一切阻力,取g=10m/s2,求: