题目内容
设地球的质量为M,半径为R,某行星的质量约为地球质量的
,半径约为地球半径的
,那么在此行星上的“第一宇宙速度”与地球上的第一宇宙速度之比为 (已知万有引力常量为G).
| 1 |
| 6 |
| 1 |
| 2 |
分析:物体在地面附近绕地球做匀速圆周运动的速度叫做第一宇宙速度,大小7.9km/s,可根据卫星在圆轨道上运行时的速度公式v=
解得.
|
解答:解:设地球质量M,某星球质量
M,地球半径r,某星球半径
r
由万有引力提供向心力做匀速圆周运动得:
卫星在圆轨道上运行时的速度公式v=
,
第一宇宙速度就是星球表面圆轨道的运行速度,
分别代入地球和某星球的各物理量得
此行星的第一宇宙速度与地球第一宇宙速度之比为
=
:3.
故答案为:
:3.
| 1 |
| 6 |
| 1 |
| 2 |
由万有引力提供向心力做匀速圆周运动得:
卫星在圆轨道上运行时的速度公式v=
|
第一宇宙速度就是星球表面圆轨道的运行速度,
分别代入地球和某星球的各物理量得
此行星的第一宇宙速度与地球第一宇宙速度之比为
| v 行 |
| v 地 |
| ||||||||
| 1 |
| 3 |
故答案为:
| 3 |
点评:本题要掌握第一宇宙速度的定义,正确利用万有引力公式列出第一宇宙速度的表达式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
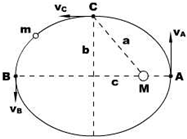 我国航天技术世界领先,天宫、神八相继发射成功,由此激发了我们对地球运动的深入研究.设地球和太阳的质量分别为m和M,地球绕太阳作椭圆运动,轨道的半长轴为a,半短轴为b,如图所示.(已知:地球的势能为
我国航天技术世界领先,天宫、神八相继发射成功,由此激发了我们对地球运动的深入研究.设地球和太阳的质量分别为m和M,地球绕太阳作椭圆运动,轨道的半长轴为a,半短轴为b,如图所示.(已知:地球的势能为 如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。