题目内容
如图所示，一列简谐波在x轴上传播，实线表示t1=0时波形，虚线表示t2=0.005s时的波形．求这列波的传播速度．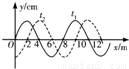
【答案】分析：由于波的传播方向未知，要分波沿x轴正方向和负方向传播两种方向研究．当波沿x轴正方向传播时，传播的最小距离为
波长，当波沿x轴正方向传播时，传播的最小距离为
波长，根据波的周期性写出波传播距离的通项，再求解波速的通项．
解答：解：若波沿x轴正方向，传播的距离为
x1=（n+
）λ，n=0，1，2，…
波速为v1=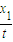
=
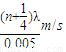=（400+1600n）m/s，n=0，1，2，…
同理，若波沿x轴负方向，传播的距离为 x2=（n+
）λ，n=0，1，2，…
波速为v2=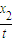
=（1200+1600n）m/s，n=0，1，2，…
答：这列波的传播速度为：波沿x轴正方向，波速为（400+1600n）m/s；若波沿x轴负方向，波速为（1200+1600n）m/s，（n=0，1，2，…）
点评：本题知道两个时刻的波形要确定波速，要考虑波的双向性和周期性，得到波速的通项，不能漏解，只得到特殊值．
波长，当波沿x轴正方向传播时，传播的最小距离为波长，根据波的周期性写出波传播距离的通项，再求解波速的通项．解答：解：若波沿x轴正方向，传播的距离为
x1=（n+
）λ，n=0，1，2，…波速为v1=
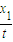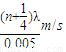==（400+1600n）m/s，n=0，1，2，…同理，若波沿x轴负方向，传播的距离为 x2=（n+
）λ，n=0，1，2，…波速为v2=
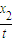=（1200+1600n）m/s，n=0，1，2，…答：这列波的传播速度为：波沿x轴正方向，波速为（400+1600n）m/s；若波沿x轴负方向，波速为（1200+1600n）m/s，（n=0，1，2，…）
点评：本题知道两个时刻的波形要确定波速，要考虑波的双向性和周期性，得到波速的通项，不能漏解，只得到特殊值．
练习册系列答案
相关题目
如图所示是一列简谐波在某一时刻的波形，则（ ）
如图所示是一列简谐波在某一时刻的波形，则在该时刻（ ）
如图所示是一列简谐波在t=0时的波形和传播距离．波沿x轴的正向传播，已知从t=0到t=2.2s时间内，质点P三次出现在波峰位置．且在t=2.2s时P质点刚好在波峰位置．求：
如图所示为一列简谐波在t1=0时刻的图象，已知质点M的振动方程为y=5sin5πt（cm），此波中质点M在t2=
（1）下列光学现象中，有全反射现象的是