题目内容
14．
如图所示为物体沿平直轨道运动时，速度随位移变化的图象，其中0～x1段的图线为一顶点在原点，开口向右的抛物线的部分，x1～x2段图线为直线，两段图线在对接处相切．则下列说法中正确的是（ ）| A． | 0～x1段，物体做加速度减小的加速运动 | |
| B． | x1～x2段，物体做加速度减小的加速运动 | |
| C． | 0～x1段，物体的平均速度为$\frac{{v}_{0}}{3}$ | |
| D． | 0～x2段，物体的平均速度为$\frac{{v}_{0}}{2}$ |
分析 对照匀变速直线运动的公式v2=2ax可分析0～x1段，物体做匀加速运动．根据x1～x2段图象的斜率分析物体的运动情况．再进一步求平均速度．
解答 解：A、0～x1段的图线为一顶点在原点，开口向右的抛物线的部分，由数学知识可得：v2=2Px．对照匀变速直线运动的公式v2=2ax可加速度一定，则0～x1段，物体做匀加速运动．故A错误．
B、x1～x2段图线为直线，则有：k=$\frac{△v}{△x}$=$\frac{△v}{△t}$•$\frac{△t}{△x}$=$\frac{a}{v}$，得：a=kv，v增大，a增大，可知物体做加速度增大的加速运动，故B错误．
C、0～x1段，物体做匀加速直线运动，平均速度为：$\overline{v}$=$\frac{0+\frac{2}{3}{v}_{0}}{2}$=$\frac{{v}_{0}}{3}$，故C正确．
D、0～x2段，物体做的不是匀变速直线运动，其平均速度不等于$\frac{{v}_{0}}{2}$．故D错误．
故选：C
点评 解决本题的关键要根据数学知识得出a与v的关系，从而分析出物体的运动性质．要知道平均速度公式$\overline{v}$=$\frac{{v}_{0}+v}{2}$只适用于匀变速直线运动．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
图是通过频闪招想得到的照片得到的照片，每个格的边长L=5cm，通过实验，记录了小球在运动途中的三个位置，如图所示，则该频闪照相的周期为0.1s小球做平抛运动的初速度为1.5m/s；过B点的速度为2.5m/s．（g=10m/s2）
如图1所示的演示实验中，A、B两球同时落地，说明平抛运动在竖直方向上是自由落体运动．某同学设计了如图2的实验：将两个质量相等的小钢球，从斜面的同一高度由静止同时释放，滑道2与光滑水平板吻接，则他将观察到的现象是两球相碰，
2．一种通信卫星需要静止在赤道上空的某一点，因此它的运行周期必须与地球的自转周期相同．已知月球绕地球运转的周期为27天，那么根据开普勒第三定律，通信卫星离地心的距离大约是月心离地心距离的（ ）倍．
| A． | 27 | B． | $\frac{1}{27}$ | C． | 9 | D． | $\frac{1}{9}$ |
9．如图1是演示简谐运动图象的装置，当盛沙漏斗下面的薄木板N被匀速地拉出时，摆动着的漏斗中漏出的沙在板上形成的曲线显示出摆的位移随时间变化的关系，板上直线OO′代表时间轴．图2是一次实验中用同一个摆长不变的摆做出的两组操作形成的曲线，若板N1和N2拉动速度用v1和v2表示，板N1和N2上曲线所代表的摆动周期用T1和T2表示，则（ ）
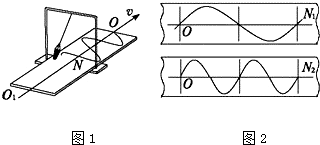
| A． | T1=2T2 | B． | 2T1=T2 | C． | v1=2v2 | D． | 2v1=v2 |
如图所示，一个半径为R的半圆透明球体放置在水平面上，一束光从A点垂直直径射入球体．已知OA=$\frac{{\sqrt{3}}}{2}$R，该球体对光的折射率为$\sqrt{2}$．则：
6．如图1所示为一足够长的光滑斜面，一定质量的滑块从斜面的底端由静止开始在一沿斜面向上的外力作用下运动，经10s的时间撤走外力，利用速度传感器在计算机上描绘了滑块在0～30s内的速度-时间图象，如图2所示．则下列说法正确的是（ ）
| A． | 滑块在0～10 s内的平均速度等于10～20 s内的平均速度 | |
| B． | 滑块在0～30 s内的位移最大 | |
| C． | 滑块在10～20 s内的加速度与20～30 s内的加速度等大反向 | |
| D． | 滑块在10～20 s内的位移与20～30 s内的位移等大反向 |
3．关于核能，下述正确的是（ ）
| A． | 它是可再生能源 | |
| B． | 它只能通过重核裂变获得 | |
| C． | 它是原子核结构发生变化时放出的能量 | |
| D． | 重核裂变的反应速度无法控制 |
