题目内容
现代观测表明，由于引力作用，恒星有“聚集”的特点，．众多的恒星组成不同层次的恒星系统，最简单的恒星系统是两颗互相绕转的双星，如图所示，两星各以一定速率绕其连线上某一点匀速转动，这样才不至于因万有引力作用而吸引在一起，已知双星质量分别为m1、m2，它们间的距离始终为L，引力常数为G，求：?（1）双星旋转的中心O到m1的距离；?
（2）双星的转动周期．?
【答案】分析：双星在相互之间的万有引力作用下，绕连线上的O点做周期相同的匀速圆周运动，根据牛顿第二定律分别对两星进行列式，来求解．
解答：解：（1）设m1到中心O的距离为x，双星的周期相同，由万有引力充当向心力，向心力大小相等得：F引=F向
知：G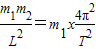
…①
G
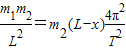…②
联立①②求解得：x=
…③
（2）由①③解得：T=2πL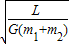
答：（1）双星旋转的中心O到m1的距离是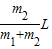
；?
（2）双星的转动周期是2πL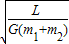
．
点评：这道题充分体现了利用双星系统的特点来解题的思路．
双星特点：1．绕同一中心转动的角速度和周期相同．
2．由相互作用力充当向心力，向心力相同．
解答：解：（1）设m1到中心O的距离为x，双星的周期相同，由万有引力充当向心力，向心力大小相等得：F引=F向
知：G
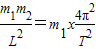…①G
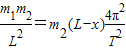…②联立①②求解得：x=
…③（2）由①③解得：T=2πL
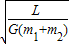
答：（1）双星旋转的中心O到m1的距离是
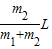；?（2）双星的转动周期是2πL
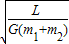．点评：这道题充分体现了利用双星系统的特点来解题的思路．
双星特点：1．绕同一中心转动的角速度和周期相同．
2．由相互作用力充当向心力，向心力相同．
练习册系列答案
名校课堂系列答案
相关题目
现代观测表明，由于引力作用，恒星有“聚集”的特点，．众多的恒星组成不同层次的恒星系统，最简单的恒星系统是两颗互相绕转的双星，如图所示，两星各以一定速率绕其连线上某一点匀速转动，这样才不至于因万有引力作用而吸引在一起，已知双星质量分别为m1、m2，它们间的距离始终为L，引力常数为G，求：?
