题目内容
（8分）两物块A、B用轻弹簧相连，质量均为2 kg，初始时弹簧处于原长，A．B两物块都以v＝6 m／s的速度在光滑的水平地面上运动，质量1 kg的物块C静止在前方，如图所示。B与C发生弹性碰撞。求在以后的运动中：
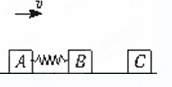
（1）物块C的速度为多大?
（2）弹簧的弹性势能的最大值是多少?
【答案】
（1）
（2）
【解析】
试题分析：（1）B与C发生弹性碰撞瞬间，由于弹簧形变明显，A仍保持原来运动状态，B与C组成的系统所受合力为零，动量机械能均守恒。设碰后瞬间B、C两者速度分别为
、
，则
根据动量守恒得：
根据机械能守恒定律得：
．
解得：
，方向与
的方向相同；
，方向与
的方向相同。
由以上分析知，在B与C发生弹性碰撞以后的运动中C以8
速度始终向右做匀速直线运动。
（2）B、C碰后， A向右做减速运动、B向右做加速运动，当二者的速度相等时弹簧的弹性势能最大．设物块A、B的共同速度为
，由动量守恒定律和机械能守恒定律得：
联立以上两式解得：
考点：本题考查考生应用动量守恒定律和机械能守恒定律解决碰撞问题的能力．
练习册系列答案
阅读快车系列答案
相关题目
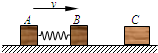两物块A、B用轻弹簧相连，质量均为2kg，初始时弹簧处于原长，A、B两物块都以v=6m/s的速度在光滑的水平地面上运动，质量4kg的物块C静止在前方，如图所示．B与C碰撞后二者会粘在一起运动．求在以后的运动中：
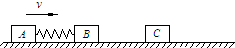两物块A、B用轻弹簧相连，质量均为2kg，初始时弹簧处于原长，A、B两物块都以v=6m/s的速度在光滑的水平地面上运动，质量4kg的物块C静止在前方，如图所示．B与C碰撞后二者立刻会粘在一起运动．求在以后的运动中：
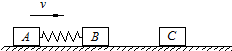两物块A、B用轻弹簧相连，质量均为2kg，初始时弹簧处于原长，A、B两物块都以v=6m/s的速度在光滑的水平地面上运动，质量4kg的物块C静止在前方，如图所示．B与C碰撞后二者立刻会粘在一起运动．求在以后的运动中：