题目内容
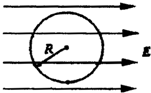 半径为R的绝缘光滑圆环固定在竖直平面内,环上套有一个带正的小珠子,该装置所在空间存在着水平向右的匀强电场,如图,已知珠子所受电场力是重力的3/4倍,将珠子从最低点由静止释放,则珠子获得的最大速度是
半径为R的绝缘光滑圆环固定在竖直平面内,环上套有一个带正的小珠子,该装置所在空间存在着水平向右的匀强电场,如图,已知珠子所受电场力是重力的3/4倍,将珠子从最低点由静止释放,则珠子获得的最大速度是分析:带正电的珠子受到重力和电场力的共同的作用,若没有速度,在空间中存在一点,该点能够使珠子静止下来,这一点就是珠子的平衡位置,是珠子具有最大动能的点.对该点的珠子进行受力分析,求出该点的位置,然后使用动能定理求出珠子的最大速度.
解答:解:如图,在珠子能够静止的一点进行受力分析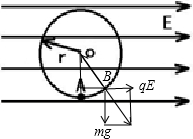
设OB与OA之间的夹角为θ,则:tanθ=
=
所以:θ=37°
珠子在等效最低点B时具有最大的动能.
珠子从A到B的过程电场力和重力做功,珠子的动能增加,即:-mgR(1-cosθ)+qER?sinθ=
m
-0
将qE=
mg,代入解得珠子所能获得的最大速度为:vm=
故答案为:
,37°

设OB与OA之间的夹角为θ,则:tanθ=
| qE |
| mg |
| 3 |
| 4 |
所以:θ=37°
珠子在等效最低点B时具有最大的动能.
珠子从A到B的过程电场力和重力做功,珠子的动能增加,即:-mgR(1-cosθ)+qER?sinθ=
| 1 |
| 2 |
| v | 2 m |
将qE=
| 3 |
| 4 |
| 0.5gR |
故答案为:
| 0.5gR |
点评:该题属于重力与电场力的复合场问题,解决问题的关键是找到带电体的等效平衡位置.属于基础题目.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
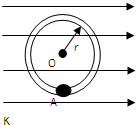 如图所示,半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一个质量为m、带正电的珠子,空间存在水平向右的匀强电场,珠子所受的电场力是其重力的
如图所示,半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一个质量为m、带正电的珠子,空间存在水平向右的匀强电场,珠子所受的电场力是其重力的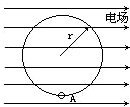 半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是其重力的
半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是其重力的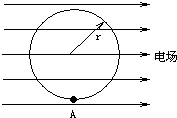 (2007?淮安模拟)半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是其重力的3/4倍.将珠子从环上最低位置A点静止释放,求:
(2007?淮安模拟)半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是其重力的3/4倍.将珠子从环上最低位置A点静止释放,求: 半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m,带正电的珠子,空间存在水平向右的匀强电场,如图所示,珠子所受静电力是其重力的3/4,将珠子从环上最低位置A点由静止释放,则珠子所能获得的最大动能Ek为( )
半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m,带正电的珠子,空间存在水平向右的匀强电场,如图所示,珠子所受静电力是其重力的3/4,将珠子从环上最低位置A点由静止释放,则珠子所能获得的最大动能Ek为( )