题目内容
2.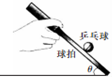 运动员手持乒乓球拍托着球沿平直跑到匀加速跑动,设球拍和球的质量分别为M、m,球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,摩擦及空气阻力不计,则( )
运动员手持乒乓球拍托着球沿平直跑到匀加速跑动,设球拍和球的质量分别为M、m,球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,摩擦及空气阻力不计,则( )| A. | 球拍对球的作用力大于mgcosθ | |
| B. | 运动员对球拍的作用力为Mgcosθ | |
| C. | 运动员的加速度为gtanθ | |
| D. | 若运动员的加速度大于gtanθ,球可能沿球拍向下运动 |
分析 由题,不计摩擦力,分析乒乓球的受力情况,作出力图,根据牛顿第二定律求解加速度和球拍对球的作用力;分析乒乓球竖直方向的受力情况,判断球能否向上运动.
解答 解:A、对乒乓球:受到重力mg和球拍的支持力N,作出力图如图,根据牛顿第二定律得:
Nsinθ=ma
Ncosθ=mg
解得,a=gtanθ,N=$\frac{mg}{cosθ}$
以球拍和球整体为研究对象,如图2,根据牛顿第二定律得:
运动员对球拍的作用力为F=$\frac{(M+m)g}{cosθ}$,故AC正确,B错误.
D、当a>gtanθ时,球将向上运动,.故D错误.
故选:AC.
点评 本题是两个作用下产生加速度的问题,分析受力情况是解答的关键,运用正交分解,根据牛顿第二定律求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.机动车的尾气含有铅等大量有害物质,并且也是造成地球“温室效应”、城市“雾霾”的重要因素之一.电动汽车因其无尾气排放且噪音小等因素,正在逐渐被人们接受.某国产品牌电动汽车的铭牌如下,已知蓄电池储存的电能等于其容量乘以输出电压,则下列说法正确的是( )
| 规格 | 后轮驱动直流电动机 |
| 车型:60″电动汽车 | 电动机额定输出功率:1675W |
| 整车质量:400kg | 电动机额定转速:600r/min |
| 蓄电池(容量:It=800Ah,输出电压:36V) | 电动机额定工作电压/电流;36V/50A |
| A. | 电动机正常工作时消耗的电功率1800W | |
| B. | 电动机的内阻为0.5Ω | |
| C. | 蓄电池充满电后储存的电能约为1.04×108J | |
| D. | 蓄电池充满电后,电动机在额定功率下工作,汽车连续行驶的时间为16h |
10. 如图所示,在矩形有界匀强磁场区域ABCD内有一质量可以忽略不计,电阻为R的闭合导线框abcd.线框在外力F的作用下,从图示位置匀速向右离开磁场.若第一次用0.2s时间拉出,电路中的电流为I1,cd边受的安培力为F1,外力所做的功率为P1,通过导线截面的电荷量为q1;第二次用0.6s时间拉出,电路中的电流为I2,cd边受的安培力为F2,外力所做的功率为P2,通过导线截面的电荷量为q 2,则( )
如图所示,在矩形有界匀强磁场区域ABCD内有一质量可以忽略不计,电阻为R的闭合导线框abcd.线框在外力F的作用下,从图示位置匀速向右离开磁场.若第一次用0.2s时间拉出,电路中的电流为I1,cd边受的安培力为F1,外力所做的功率为P1,通过导线截面的电荷量为q1;第二次用0.6s时间拉出,电路中的电流为I2,cd边受的安培力为F2,外力所做的功率为P2,通过导线截面的电荷量为q 2,则( )
 如图所示,在矩形有界匀强磁场区域ABCD内有一质量可以忽略不计,电阻为R的闭合导线框abcd.线框在外力F的作用下,从图示位置匀速向右离开磁场.若第一次用0.2s时间拉出,电路中的电流为I1,cd边受的安培力为F1,外力所做的功率为P1,通过导线截面的电荷量为q1;第二次用0.6s时间拉出,电路中的电流为I2,cd边受的安培力为F2,外力所做的功率为P2,通过导线截面的电荷量为q 2,则( )
如图所示,在矩形有界匀强磁场区域ABCD内有一质量可以忽略不计,电阻为R的闭合导线框abcd.线框在外力F的作用下,从图示位置匀速向右离开磁场.若第一次用0.2s时间拉出,电路中的电流为I1,cd边受的安培力为F1,外力所做的功率为P1,通过导线截面的电荷量为q1;第二次用0.6s时间拉出,电路中的电流为I2,cd边受的安培力为F2,外力所做的功率为P2,通过导线截面的电荷量为q 2,则( )| A. | I1:I2=3:1 | B. | F1:F2=1:1 | C. | P1:P2=9:1 | D. | q 1:q 2=1:3 |
14. 如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下极板接地,静电计所带电量很少,可被忽略.一带负电油滴被固定于电容器中的P点,现将平行板电容器的下极板竖直向上移动一小段距离,则( )
如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下极板接地,静电计所带电量很少,可被忽略.一带负电油滴被固定于电容器中的P点,现将平行板电容器的下极板竖直向上移动一小段距离,则( )
 如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下极板接地,静电计所带电量很少,可被忽略.一带负电油滴被固定于电容器中的P点,现将平行板电容器的下极板竖直向上移动一小段距离,则( )
如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下极板接地,静电计所带电量很少,可被忽略.一带负电油滴被固定于电容器中的P点,现将平行板电容器的下极板竖直向上移动一小段距离,则( )| A. | 平行板电容器的电容值将变大 | |
| B. | 静电计指针张角变大 | |
| C. | 带电油滴所受电场力将变大 | |
| D. | 若先将上极板与电源正极的导线断开,再将下极板向下移动一小段距离,则带电油滴所受电场力将变小 |
12.在电磁学理论建立的过程中,有许多伟大的科学家做出了贡献.关于科学家和他们的贡献,下列说法正确的是( )
| A. | 麦克斯韦认为,磁场变化时会在空间激发一种电场 | |
| B. | 奥斯特梦圆电生磁,终于发现了电场感应现象 | |
| C. | 伏特发现了电流热效应的规律,并定性地给出了电能和内能之间的转化关系 | |
| D. | 法拉第通过实验发现了在磁场中产生电流的条件,并总结出了确定感应电流方向的方法 |
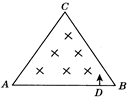 在边长为2a的正△ABC内存在垂直纸面向里的磁感强度为B的匀强磁场,有一带正电q,质量为m的粒子从距A点$\sqrt{3}$a的D点垂直AB方向进入磁场,如图所示,求:
在边长为2a的正△ABC内存在垂直纸面向里的磁感强度为B的匀强磁场,有一带正电q,质量为m的粒子从距A点$\sqrt{3}$a的D点垂直AB方向进入磁场,如图所示,求: 在做“探究加速度与力、质量的关系”实验时,采用如图所示的实验装置,让重物通过轻绳拖动小车在长木板上做匀加速直线运动.其中小车质量用M表示,重物质量用m表示,加速度用a表示.
在做“探究加速度与力、质量的关系”实验时,采用如图所示的实验装置,让重物通过轻绳拖动小车在长木板上做匀加速直线运动.其中小车质量用M表示,重物质量用m表示,加速度用a表示.