题目内容
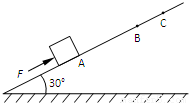
如图所示,小木块在沿斜面向上的恒定外力F作用下,从A点由静止开始做匀加速运动,前进了0.45m抵达B点时,立即撤去外力.此后小木块又前进0.15m到达C点,速度为零.已知木块与斜面间的动摩擦因数μ=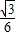 ,木块质量m=1kg.求:
,木块质量m=1kg.求:(1)木块向上经过B点时速度为多大?
(2)木块在AB段所受的外力F多大?(取g=10m/s2)
(3)木块回到A点的速度v为多大?
【答案】分析:(1)对小滑块加速和减速过程分别受力分析,加速过程受推力、重力、支持力和摩擦力,减速过程,推力撤销,其余力不变;然后对两个过程运用牛顿第二定律求出加速度,再根据速度位移公式列式求解;
(2)依据第一问的解答,可以进一步得到外力F的大小;
(3)木块下降过程,先受力分析,受重力、支持力和摩擦力,根据牛顿第二定律求解加速度,再根据运动学公式求解木速度.
解答:解:(1)小滑块加速过程受推力、重力、支持力和摩擦力,根据牛顿第二定律,有
F-mgsinθ-μmgcosθ=ma1 ①
小滑块减速过程受重力、支持力和摩擦力,根据牛顿第二定律,有
mgsinθ+μmgcosθ=ma2 ②
对于加速过程,根据运动学公式,有
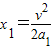 ③
③
对于减速过程,根据运动学公式,同样有
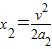 ④
④
有①②③④解得
v=1.5 m/s
F=10 N
故木块向上经过B点时速度为1.5m/s;
(2)木块在AB段所受的外力F为10N;
(3)木块下降过程受重力、支持力和摩擦力,根据牛顿第二定律,有
mgsinθ-μmgcosθ=ma3 ⑤
根据速度位移公式,有
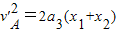 ⑥
⑥
解得
v′A=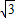 m/s
m/s
即木块回到A点的速度v为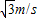 .
.
点评:本题关键是对木块受力分析,根据牛顿第二定律求出各个时间段的加速度,然后根据运动学公式列式求解.
(2)依据第一问的解答,可以进一步得到外力F的大小;
(3)木块下降过程,先受力分析,受重力、支持力和摩擦力,根据牛顿第二定律求解加速度,再根据运动学公式求解木速度.
解答:解:(1)小滑块加速过程受推力、重力、支持力和摩擦力,根据牛顿第二定律,有
F-mgsinθ-μmgcosθ=ma1 ①
小滑块减速过程受重力、支持力和摩擦力,根据牛顿第二定律,有
mgsinθ+μmgcosθ=ma2 ②
对于加速过程,根据运动学公式,有
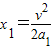 ③
③对于减速过程,根据运动学公式,同样有
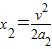 ④
④有①②③④解得
v=1.5 m/s
F=10 N
故木块向上经过B点时速度为1.5m/s;
(2)木块在AB段所受的外力F为10N;
(3)木块下降过程受重力、支持力和摩擦力,根据牛顿第二定律,有
mgsinθ-μmgcosθ=ma3 ⑤
根据速度位移公式,有
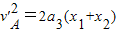 ⑥
⑥解得
v′A=
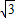 m/s
m/s即木块回到A点的速度v为
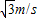 .
.点评:本题关键是对木块受力分析,根据牛顿第二定律求出各个时间段的加速度,然后根据运动学公式列式求解.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 如图所示,小木块在沿斜面向上的恒定外力F作用下,从A点由静止开始做匀加速运动,前进了0.45m抵达B点时,立即撤去外力.此后小木块又前进0.15m到达C点,速度为零.已知木块与斜面间的动摩擦因数μ=
如图所示,小木块在沿斜面向上的恒定外力F作用下,从A点由静止开始做匀加速运动,前进了0.45m抵达B点时,立即撤去外力.此后小木块又前进0.15m到达C点,速度为零.已知木块与斜面间的动摩擦因数μ= 如图所示,小木块在沿斜面向上的恒定外力F作用下,从A点由静止开始作匀加速运动,前进了0.45m抵达B点时,立即撤去外力.此后小木块又前进0.15m到达C点,速度为零.已知木块与斜面动摩擦因数μ=
如图所示,小木块在沿斜面向上的恒定外力F作用下,从A点由静止开始作匀加速运动,前进了0.45m抵达B点时,立即撤去外力.此后小木块又前进0.15m到达C点,速度为零.已知木块与斜面动摩擦因数μ= ,木块质量m=1kg。
,木块质量m=1kg。
 ,木块质量m=1kg。
,木块质量m=1kg。
 ,木块质量m=1kg。
,木块质量m=1kg。