题目内容
20. 如图所示,光滑的斜槽轨道AB的B端切线水平,在B点静止放置一个质量为m2的小球,另一个质量为m1的小球从斜槽上某点A静止释放下滑,与m2发生无机械能损失的正碰,碰后两球落到水平面上,落地点到O的距离之比为OP:OM=3:1,则两球质量之比m1:m2可能为( )
如图所示,光滑的斜槽轨道AB的B端切线水平,在B点静止放置一个质量为m2的小球,另一个质量为m1的小球从斜槽上某点A静止释放下滑,与m2发生无机械能损失的正碰,碰后两球落到水平面上,落地点到O的距离之比为OP:OM=3:1,则两球质量之比m1:m2可能为( )| A. | 3:1 | B. | 3:2 | C. | 3:5 | D. | 1:7 |
分析 根据平抛运动的规律得到两球碰后速度大小关系,由于碰后m1球可能沿原方向运动,也可能反弹,要分两种情况,由动量守恒定律和机械能守恒定律结合求解.
解答 解:设碰撞前m1小球的速度为v0,碰后瞬间m1、m2的速度分别为v1、v2.
取水平向左为正方向,由动量守恒定律和机械能守恒定律得
m1v0=m1v1+m1v2,
$\frac{1}{2}$m1v02=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22,
解得:v1=$\frac{{m}_{1}-{m}_{2}}{{m}_{1}+{m}_{v}}$v0,v2=$\frac{2{m}_{1}}{{m}_{1}+{m}_{2}}$v0.
碰后两球离开轨道后都做平抛运动,运动时间相等,由x=v0t知,|v1|:v2=OM:OP=1:3
若碰后瞬间m1的速度向左,则 v1:v2=1:3
联立解得 m1:m2=3:1
若碰后瞬间m1的速度向右,则-v1:v2=1:3
联立解得 m1:m2=3:5
故选:AC
点评 本题是弹性碰撞问题,要知道碰撞过程遵守动量守恒定律与机械能守恒定律,要注意碰后m1球的速度有两种可能,不能漏解.

练习册系列答案
相关题目
11.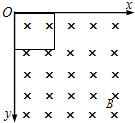 如图所示,一边长为L,质量为m,电阻为R的正方形金属框竖直放置在磁场中,磁场方向垂直方框平面向里,磁感应强度B的大小随y的变化规律为B=B0+ky(k为常数且大于零),同一水平面上的磁感应强度相同.现将方框从图示位置水平向右抛出,已知重力加速度为g,磁场区域足够大,不计空气阻力,则( )
如图所示,一边长为L,质量为m,电阻为R的正方形金属框竖直放置在磁场中,磁场方向垂直方框平面向里,磁感应强度B的大小随y的变化规律为B=B0+ky(k为常数且大于零),同一水平面上的磁感应强度相同.现将方框从图示位置水平向右抛出,已知重力加速度为g,磁场区域足够大,不计空气阻力,则( )
 如图所示,一边长为L,质量为m,电阻为R的正方形金属框竖直放置在磁场中,磁场方向垂直方框平面向里,磁感应强度B的大小随y的变化规律为B=B0+ky(k为常数且大于零),同一水平面上的磁感应强度相同.现将方框从图示位置水平向右抛出,已知重力加速度为g,磁场区域足够大,不计空气阻力,则( )
如图所示,一边长为L,质量为m,电阻为R的正方形金属框竖直放置在磁场中,磁场方向垂直方框平面向里,磁感应强度B的大小随y的变化规律为B=B0+ky(k为常数且大于零),同一水平面上的磁感应强度相同.现将方框从图示位置水平向右抛出,已知重力加速度为g,磁场区域足够大,不计空气阻力,则( )| A. | 线框将一直做曲线运动 | |
| B. | 线框最终将做直线运动 | |
| C. | 线框最终的速度大于$\frac{mgR}{{k}^{2}{L}^{4}}$ | |
| D. | 线框中产生的感应电流沿顺时针方向 |
15. 在光电效应实验中,某同学用同一光电管在不同实验条件下得到了三条光电流与电压之间的关系曲线(甲光、乙光、丙光)如图所示,则可判断出( )
在光电效应实验中,某同学用同一光电管在不同实验条件下得到了三条光电流与电压之间的关系曲线(甲光、乙光、丙光)如图所示,则可判断出( )
 在光电效应实验中,某同学用同一光电管在不同实验条件下得到了三条光电流与电压之间的关系曲线(甲光、乙光、丙光)如图所示,则可判断出( )
在光电效应实验中,某同学用同一光电管在不同实验条件下得到了三条光电流与电压之间的关系曲线(甲光、乙光、丙光)如图所示,则可判断出( )| A. | 乙光的光照强度大于甲光的光照强度 | |
| B. | 乙光的波长大于丙光的波长 | |
| C. | 乙光对应的截止频率大于丙光的截止频率 | |
| D. | 甲光对应的光电子最大初动能大于丙光的光电子最大初动能 |
5.在绕地球做匀速圆周运动的太空实验室内,下列仪器中可正常使用的有( )
| A. | 摆钟 | B. | 天平 | C. | 弹簧测力计 | D. | 水银温度计 |
12.对于经典力学理论,下列说法正确的是( )
| A. | 由于相对论、量子论的提出,经典力学已经失去了它的意义 | |
| B. | 经典力学在今天广泛应用,它的正确性无可怀疑,仍是普遍适用的 | |
| C. | 经典力学在历史上起了巨大的作用,随着物理学的发展而逐渐过时,成为一种古老的理论 | |
| D. | 经典力学在宏观低速运动中,引力不太大时适用 |
9. 如图所示,用r表示两个分子间的距离,用Ep表示两个分子之间的势能,当r=r0时两分子间斥力等于引力,设两个分子相距很远时Ep=0,则( )
如图所示,用r表示两个分子间的距离,用Ep表示两个分子之间的势能,当r=r0时两分子间斥力等于引力,设两个分子相距很远时Ep=0,则( )
 如图所示,用r表示两个分子间的距离,用Ep表示两个分子之间的势能,当r=r0时两分子间斥力等于引力,设两个分子相距很远时Ep=0,则( )
如图所示,用r表示两个分子间的距离,用Ep表示两个分子之间的势能,当r=r0时两分子间斥力等于引力,设两个分子相距很远时Ep=0,则( )| A. | 当r<r0时,Ep随r的增大而增大 | B. | 当r>r0时,Ep随r的增大而增大 | ||
| C. | 当r<r0时,Ep不随r的变化而变化 | D. | 当r=r0时,Ep=0 |
 某探究小组为探究向心力与线速度、角速度、圆周半径等大小关系,利用两个相同材质可绕竖直轴转动的水平转盘和两个相同的长方体小橡皮擦进行实验.如图所示,转盘半径分别为2r和r,A点在大转盘的边缘处、B点在大转盘上离转轴距离为r处,C点在小转盘的边缘处,橡皮擦与转盘间的最大静摩擦力是其所受重力的?倍,大转盘通过皮带带动小转盘无打滑地转动.现将一橡皮擦放置在A处,
某探究小组为探究向心力与线速度、角速度、圆周半径等大小关系,利用两个相同材质可绕竖直轴转动的水平转盘和两个相同的长方体小橡皮擦进行实验.如图所示,转盘半径分别为2r和r,A点在大转盘的边缘处、B点在大转盘上离转轴距离为r处,C点在小转盘的边缘处,橡皮擦与转盘间的最大静摩擦力是其所受重力的?倍,大转盘通过皮带带动小转盘无打滑地转动.现将一橡皮擦放置在A处,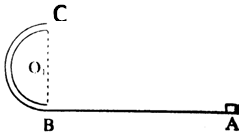 如图所示,半径为R=0.4m的半圆形弯管竖直放置,管的内径远小于弯管的半径且管内光滑,弯管与水平直轨道BA相切于B点,质量为M=0.5kg的物块静止在水平轨道A点,A、B间距离s=2m,物块与水平面间的动摩擦因数μ=0.2,对物块施加一恒力F使其由静止开始从A点加速运动,运动到B点时撤去推力,物块从B点进入半圆轨道,恰能运动到轨道最高点C.(g=10m/s2)问:
如图所示,半径为R=0.4m的半圆形弯管竖直放置,管的内径远小于弯管的半径且管内光滑,弯管与水平直轨道BA相切于B点,质量为M=0.5kg的物块静止在水平轨道A点,A、B间距离s=2m,物块与水平面间的动摩擦因数μ=0.2,对物块施加一恒力F使其由静止开始从A点加速运动,运动到B点时撤去推力,物块从B点进入半圆轨道,恰能运动到轨道最高点C.(g=10m/s2)问: 如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点,测得四个时刻物体的瞬时速度记录在下表中,取g=10m/s2.求:
如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点,测得四个时刻物体的瞬时速度记录在下表中,取g=10m/s2.求: