��Ŀ����
1��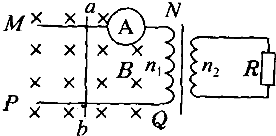 ��ͼ��ʾ��MN��PQ��������ˮƽ���ڡ�ƽ�з��õĹ⻬�������죬������Ҷ˽������ѹ����ԭ��Ȧ����ѹ���ĸ���Ȧ����ֵΪR=0.5���ĵ�����ɱպϻ�·����ѹ����ԭ����Ȧ����֮��n1��n2=2��1���������ΪL=0.5m������Ϊm=1kg�ĵ����ab��ֱMN��PQ���ڵ����ϣ���ˮƽ���������£���t=0ʱ�̿�ʼ�������˶������ٶ���ʱ�ʱ仯�Ĺ�����v=2sin$\frac{��}{2}$t��m/s������֪��ֱ���ƽ�����µ���ǿ�ų��ĴŸ�Ӧǿ�ȴ�СΪB=1T�����졢����������ߺ���Ȧ�ĵ�������ƣ�������Ϊ���뽻���������������ʼ���ڴų����˶�����
��ͼ��ʾ��MN��PQ��������ˮƽ���ڡ�ƽ�з��õĹ⻬�������죬������Ҷ˽������ѹ����ԭ��Ȧ����ѹ���ĸ���Ȧ����ֵΪR=0.5���ĵ�����ɱպϻ�·����ѹ����ԭ����Ȧ����֮��n1��n2=2��1���������ΪL=0.5m������Ϊm=1kg�ĵ����ab��ֱMN��PQ���ڵ����ϣ���ˮƽ���������£���t=0ʱ�̿�ʼ�������˶������ٶ���ʱ�ʱ仯�Ĺ�����v=2sin$\frac{��}{2}$t��m/s������֪��ֱ���ƽ�����µ���ǿ�ų��ĴŸ�Ӧǿ�ȴ�СΪB=1T�����졢����������ߺ���Ȧ�ĵ�������ƣ�������Ϊ���뽻���������������ʼ���ڴų����˶�������1����t=1sʱ�̵�������ʾ����
��2������R�����ĵĵ繦�ʣ�
��3����t=0��1=3s��ʱ����ˮƽ���������Ĺ�W��
���� ��1�����ݵ綯��ΪE=BLv=BL2sin$\frac{��t}{2}$�������t=1sʱ�ĵ�ѹ���ֵ���Ӷ������Чֵ�����ݱ�ѹ��ԭ����Ȧ��ѹ����������Ȧ�����Ĺ�ϵ��⣻
��2������P=I2R���ʣ�
��3�����ݶ��ܶ������ˮƽ���������Ĺ�W��
��� �⣺��1�������⣬�ٶȱ仯����Ϊv=2sin$\frac{��}{2}$t��m/s����������ĵ綯��ΪE=BLv=BL��2sin$\frac{��t}{2}$����t=1sʱ���綯��ΪEm=1v����ԭ��Ȧ��ѹΪU1m=1v������Чֵ${U}_{1}=\frac{\sqrt{2}}{2}V$��
����$\frac{{U}_{1}}{{U}_{2}}=\frac{{n}_{1}}{{n}_{2}}$�ã�${U}_{2}=\frac{\sqrt{2}}{4}V$������t=1sʱ�̸���Ȧ�ĵ�������������ʾ��${I}_{2}=\frac{{U}_{2}}{R}=\frac{\sqrt{2}}{2}A$��
����$\frac{{I}_{1}}{{I}_{2}}=\frac{{n}_{2}}{{n}_{1}}$�ã�${I}_{1}=\frac{\sqrt{2}}{4}A$
��2������R�����ĵĵ繦��P=${{I}_{2}}^{2}R=��\frac{\sqrt{2}}{2}��^{2}��0.5=0.25W$��
��3�����ݶ��ܶ����У�w��-w��=$\frac{1}{2}$mv2������w��=w��+$\frac{1}{2}$mv2��
��v=2sin$\frac{��}{2}$t����֪��t=0ʱ��v=0��t=3sʱ��v=-2m/s��
��������������w��=U2I2t=0.75J
��ã�w��=2.75J
�𣺣�1����t=1sʱ�̵�������ʾ��Ϊ$\frac{\sqrt{2}}{4}A$��
��2������R�����ĵĵ繦��Ϊ0.25W��
��3����t=0��1=3s��ʱ����ˮƽ���������Ĺ�Ϊ2.75J��
���� ֪��������и�Ÿ��߲�������ʽ���������Ӧ��E=BLv����ѹ����ʽ���������ɼ�����ȷ���⣬֪����������������������ȷ����Ĺؼ���

 С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д�| A�� | Բ | B�� | ��Բ | C�� | ������ | D�� | ֱ�� |
| A�� | ����ļ��ٶȱ��ֲ��䣬����һ����ֱ���˶� | |
| B�� | ������ٶȱ仯Խ�죬���ٶ�һ��Խ�� | |
| C�� | ��ֱ���˶������壬���ٶȼ�С���ٶ�һ������ | |
| D�� | ����������Բ���˶�ʱ�������ʱ�����ٶȱ仯��һ����ͬ |
| A�� | mv | B�� | $\frac{1}{2}$mv | C�� | mv2 | D�� | $\frac{1}{2}$mv2 |
| A�� | F������ | B�� | F�dz��� | ||
| C�� | ����������ɼ�ľ��룬��F��С | D�� | ����������ɼ�ľ��룬��F���� |
 ��ͼ��ʾ��������ˮƽ�����ϵ����M��N�ֱ��ܵ�F��2Fˮƽ���������ã���M��N����ֹ�����������N��Ħ������С�ͷ���ֱ��ǣ�������
��ͼ��ʾ��������ˮƽ�����ϵ����M��N�ֱ��ܵ�F��2Fˮƽ���������ã���M��N����ֹ�����������N��Ħ������С�ͷ���ֱ��ǣ�������| A�� | F���������� | B�� | F���������� | C�� | 2F���������� | D�� | 2F���������� |
 ��ͼ��ʾ������m=2kg��С���ó�L=5m������ϸ�������ھ�ˮƽ�����H=10m��O�㣮�ֽ�ϸ����ֱ��ˮƽ״̬��A�����ٶ��ͷ�С���˶�������O�����·�B��ʱϸ��ǡ�ö��ѣ�����С����ƽ���˶�������ˮƽ������C�㣮���ƿ����������������ٶ�gȡ10m/s2����
��ͼ��ʾ������m=2kg��С���ó�L=5m������ϸ�������ھ�ˮƽ�����H=10m��O�㣮�ֽ�ϸ����ֱ��ˮƽ״̬��A�����ٶ��ͷ�С���˶�������O�����·�B��ʱϸ��ǡ�ö��ѣ�����С����ƽ���˶�������ˮƽ������C�㣮���ƿ����������������ٶ�gȡ10m/s2���� ��ͼ��ʾ��б�����Ϊ��=37�㣬����1����б��������崦������1��б��䶯Ħ������Ϊ��=0.5��һ���ܳ��IJ����쳤��������������⻬���ʵ�С�����֣���һ�˹̶�������1�ϣ���һ�˹̶�������2�ϣ�б���Ϸ���������б��ƽ�У�����2�¶˹̶�һ����Ϊh�������������¶�˩��С����3�ϣ�����1��2��3������֮��Ϊ4��1��5����ʼʱ������סС����3��С����3������ĸ߶�ҲΪh����ʱ���������պ���������֪���崥�غ�����ֹͣ�˶������ٷ������������ٶ�Ϊg=10m/s2 ��С����3�Ӿ�ֹͻȻ���ֺ�����1�����ϻ���������Ϊ��������
��ͼ��ʾ��б�����Ϊ��=37�㣬����1����б��������崦������1��б��䶯Ħ������Ϊ��=0.5��һ���ܳ��IJ����쳤��������������⻬���ʵ�С�����֣���һ�˹̶�������1�ϣ���һ�˹̶�������2�ϣ�б���Ϸ���������б��ƽ�У�����2�¶˹̶�һ����Ϊh�������������¶�˩��С����3�ϣ�����1��2��3������֮��Ϊ4��1��5����ʼʱ������סС����3��С����3������ĸ߶�ҲΪh����ʱ���������պ���������֪���崥�غ�����ֹͣ�˶������ٷ������������ٶ�Ϊg=10m/s2 ��С����3�Ӿ�ֹͻȻ���ֺ�����1�����ϻ���������Ϊ�������� ��ͼ��ʾ���ڰ뾶ΪR��Բ�α߽��ڴ�����ֱ���ϵ���ǿ�糡���糡ǿ��E=1��106T����Բ��Ϊ����ԭ�㽨��ֱ������ϵ��������ԭ��ֱ�����ֱ���ϡ���ֱ���¡�ˮƽ����ˮƽ����ͬʱ�׳��ĸ��������С��С��ĵ����q=8��10-12C������m=1��10-6kg�����ǵij��ٶȴ�С��Ϊv0=4m/s�����Կ����������������ٶ�g=10m/s2����
��ͼ��ʾ���ڰ뾶ΪR��Բ�α߽��ڴ�����ֱ���ϵ���ǿ�糡���糡ǿ��E=1��106T����Բ��Ϊ����ԭ�㽨��ֱ������ϵ��������ԭ��ֱ�����ֱ���ϡ���ֱ���¡�ˮƽ����ˮƽ����ͬʱ�׳��ĸ��������С��С��ĵ����q=8��10-12C������m=1��10-6kg�����ǵij��ٶȴ�С��Ϊv0=4m/s�����Կ����������������ٶ�g=10m/s2����