题目内容
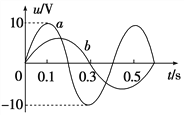
【题目】如图(a)所示，在空间有一坐标系xoy，直线OP与x轴正方向的夹角为30°，第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ，直线OP是它们的边界，OP上方区域Ⅰ中磁场的磁感应强度为B，一质量为m，电荷量为+q的质子(不计重力及质子对磁场的影响)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域Ⅰ，质子先后通过磁场区域Ⅰ和Ⅱ后，恰好垂直于x轴进入第四象限，第四象限存在沿-x轴方向的特殊电场，电场强度E的大小与横坐标x的关系如图（b）所示，试求:
(1)区域Ⅱ中磁场的磁感应强度大小 ；
(2)质子再次到达y轴时的速度大小和方向。
【答案】 （1）
；（2）
；方向向左下方与y轴负向成
（
）的夹角
【解析】
试题分析: （1）由几何关系知：质子再次回到OP时应平行于x轴正向进入Ⅱ区，设质子从OP上的C点进入Ⅱ区后再从D点垂直x轴进入第四象限，轨迹如图。
由几何关系可知：O1C⊥OX，O1C与OX的交点O2即为Ⅱ内圆弧的圆心，
等边三角形。
设质子在Ⅰ区圆运动半径为
，在Ⅱ区圆运动半径为
，
则：
由
得：
， 同理得：
即区域Ⅱ中磁场的磁感应强度：
（2）D点坐标： 
质子从D点再次到达y轴的过程，
设质子再次到达y轴时的速度大小为
，
由动能定理：
得：
因粒子在y轴方向上不受力，故在y轴方向上的分速度不变
如图有： 
即方向向左下方与y轴负向成（）的夹角
【题目】简谐运动是一种周期性运动，其周期与振动物体的质量的平方根成正比，与振动系统的振动系数的平方根成反比，而与振幅无关，即： 
．
试论证分析如下问题：
（
）如图甲，摆长为
、摆球质量为
的单摆在
间做小角度的自由摆动，当地重力加速度为
．
a．当摆球运动到
点时，摆角为
，画出摆球受力的示意图，并写出此时刻摆球受到的回复 大小；
b．请结合简谐运动的特点，证明单摆在小角度摆动时周期为
．
（提示：用弧度制表示角度，当角
很小时， 
， 
角对应的弧长与它所对的弦长也近似相等）
|
|
|
图甲 | 图乙 | 图丙 |
（
）类比法、等效法等都是研究和学习物理过程中常用的重要方法．长为
的轻质绝缘细线下端系着一个带电量为
，质量为
的小球．将该装置处于场强大小为
的竖直向下的匀强电场中，如图乙所示；将该装置处于磁感应强度大小为
，方向垂直于纸面向里的匀强磁场中，如图丙所示．带电小球在乙、丙图中均做小角度的简谐运动．请分析求出带电小球在乙、丙两图中振动的周期．
