题目内容
11. 传送带以恒定速度v=4m/s顺时针运行,传送带与水平面的夹角θ=37°.现将质量m=2kg的小物品轻放在其底端(小物品可看成质点),平台上的人通过一根轻绳用恒力F=20N拉小物品,经过一段时间物品被拉到离地面高为H=1.8m的平台上,如图所示.已知物品与传送带之间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力,g取10m/s2,已知sin 37°=0.6,cos 37°=0.8.
传送带以恒定速度v=4m/s顺时针运行,传送带与水平面的夹角θ=37°.现将质量m=2kg的小物品轻放在其底端(小物品可看成质点),平台上的人通过一根轻绳用恒力F=20N拉小物品,经过一段时间物品被拉到离地面高为H=1.8m的平台上,如图所示.已知物品与传送带之间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力,g取10m/s2,已知sin 37°=0.6,cos 37°=0.8.问:物品从传送带底端运动到平台上所用的时间是多少?
分析 对物品进行受力分析,求出合外力,再根据牛顿第二定律求加速度,注意需要根据物品与传送带间速度大小判定滑动摩擦力的方向.
解答 解:物品在达到传送带速度之前,由受力情况,据牛顿定律有:
F+μmgcos37°-mgsin37°=ma1
解得:a1=8m/s2
匀加速过程,设用时为t,则:
v=a1t
匀加速位移:x=$\frac{1}{2}{a}_{1}{t}^{2}$
得:t=0.5s,x=1m
随后由受力情况,据牛顿第二定律有:F-μmgcos37°-mgsin37°=ma2
解得:a1=0,即物品随传送带匀速上升
位移:${x}_{1}=\frac{H}{sin37°}$-x=$\frac{1.8}{0.6}-1=2m$
用时为:t1=$\frac{{x}_{1}}{v}$=$\frac{2}{4}$=0.5s
故总时间:t总=t+t1=0.5+0.5=1s
答:物品从传送带底端运动到平台上所用的时间是1s.
点评 本题关键是受力分析后,根据牛顿第二定律求解出加速度,然后根据运动学公式列式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.如图所示是某物体做直线运动的v-t图象,则该物体( )
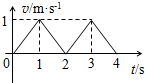

| A. | 做匀速直线运动 | B. | 做匀加速直线运动 | ||
| C. | 一直朝某一方向运动 | D. | 在某一线段上做两个来回运动 |
6. 将重为20N的物体放在倾角为30°的粗糙斜面上,物体的一端与固定在斜面上的轻弹簧连接(如图).若物体与斜面间最大静摩擦力为12N,则物体保持静止时弹簧对物体的弹力( )
将重为20N的物体放在倾角为30°的粗糙斜面上,物体的一端与固定在斜面上的轻弹簧连接(如图).若物体与斜面间最大静摩擦力为12N,则物体保持静止时弹簧对物体的弹力( )
 将重为20N的物体放在倾角为30°的粗糙斜面上,物体的一端与固定在斜面上的轻弹簧连接(如图).若物体与斜面间最大静摩擦力为12N,则物体保持静止时弹簧对物体的弹力( )
将重为20N的物体放在倾角为30°的粗糙斜面上,物体的一端与固定在斜面上的轻弹簧连接(如图).若物体与斜面间最大静摩擦力为12N,则物体保持静止时弹簧对物体的弹力( )| A. | 可以是22N,方向沿斜面向下 | B. | 不可能是零 | ||
| C. | 可以是2N,方向沿斜面向下 | D. | 可以是2N,方向沿斜面向上 |
20.做“验证牛顿第二定律”的实验中,设小车质量和车上钩码的质量之和为M,砂及砂桶的总质量为m,分别得出如图中a、b、c、d四个图线,其中图a、b、c是a-F图线,图d是a-$\frac{1}{M}$图线,则以下说法中正确的是( )


| A. | a和b较好地把握了实验条件M>>m | |
| B. | c和d则没有把握好实验条件M>>m | |
| C. | a长木板的倾角太大,而b长木板角度太小 | |
| D. | a、b、c都较好地完成了平衡摩擦力的操作 |
1. 如图所示,变压器输入有效值恒定的电压,副线圈匝数可调,输出电压通过输电线送给用户(电灯等用电器),R表示输电线的电阻,则( )
如图所示,变压器输入有效值恒定的电压,副线圈匝数可调,输出电压通过输电线送给用户(电灯等用电器),R表示输电线的电阻,则( )
 如图所示,变压器输入有效值恒定的电压,副线圈匝数可调,输出电压通过输电线送给用户(电灯等用电器),R表示输电线的电阻,则( )
如图所示,变压器输入有效值恒定的电压,副线圈匝数可调,输出电压通过输电线送给用户(电灯等用电器),R表示输电线的电阻,则( )| A. | 用电器增加时,变压器输出电压增大 | |
| B. | 要提高用户的电压,滑动触头P应向上滑 | |
| C. | 用电器增加时,输电线的热损耗减少 | |
| D. | 用电器增加时,变压器的输入功率增加 |
 如图所示,闭合开关S,调节滑动变阻 器滑片P,当理想电流表示数为0.50A 时,理想电压表示数为7.5V.已知电源 内阻为3.0a则电源电动动势是9V,电源内阻消耗的功率是0.75W.
如图所示,闭合开关S,调节滑动变阻 器滑片P,当理想电流表示数为0.50A 时,理想电压表示数为7.5V.已知电源 内阻为3.0a则电源电动动势是9V,电源内阻消耗的功率是0.75W.
 甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动.质点甲做初速度为零,加速度大小为a1的匀加速直线运动.质点乙做初速度为v0,加速度大小为a2的匀减速直线运动至速度减为零保持静止.甲、乙两质点在运动过程中的位置x-速度v图象如图所示,虚线与对应的坐标轴垂直.
甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动.质点甲做初速度为零,加速度大小为a1的匀加速直线运动.质点乙做初速度为v0,加速度大小为a2的匀减速直线运动至速度减为零保持静止.甲、乙两质点在运动过程中的位置x-速度v图象如图所示,虚线与对应的坐标轴垂直.