题目内容
A、B两行星在同一平面内绕同一恒星做匀速圆周运动,运行方向相同,A的轨道半径为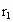 ,B的轨道半径为
,B的轨道半径为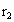 .已知恒星质量为M,恒星对行星的引力远大于行星间的引力,两行星的轨道半径
.已知恒星质量为M,恒星对行星的引力远大于行星间的引力,两行星的轨道半径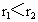 .若在某一时刻两行星相距最近,试求:
.若在某一时刻两行星相距最近,试求:
(1)再经过多少时间两行星距离又最近?
(2)再经过多少时间两行星距离最远?
答案:略
解析:
解析:
|
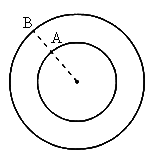
解: (1)A、B两行星在如图所示位置时距离最近,这时A、B与恒星在同一条圆半径上, A、B运动方向相同,A更靠近恒星,A的转动角速度大、周期短,如果经过时间t,A、B与恒星连线半径转过的角度相差2π的整数倍,则A、B与恒星又位于同一条圆半径上,距离最近.设 A、B的角速度分别为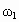 、 、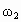 ,经过时间t,A转过的角度为 ,经过时间t,A转过的角度为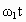 ,B转过的角度为 ,B转过的角度为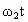 .A、B距离最近的条件是: .A、B距离最近的条件是: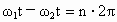 (n=1,2,3…) (n=1,2,3…)
恒星对行星的万有引力提供向心力,则
由此得出 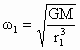 , ,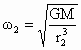
求得 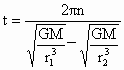 (n=1,2,3…) (n=1,2,3…)
(2)如果经过时间
得 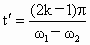 把 把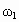 、 、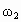 代入得: 代入得:
大多数物理问题具有单一的确定解,然而有些物理问题的解并不惟一,而有多个解.甚至有无穷多个解.对于这类物理问题,倘若物理过程不清,便可能只得出特解,而导致漏解.一般说来,周期性过程的物理问题,通常具有多解的特征,分析多解问题的基本思路是:在分析物理过程的基础上,建立清晰的物理图景,根据物理图景列方程,求出物理量的通解表达式,本题中判定 A、B相距最近、最远的条件是解题的关键. |

练习册系列答案
相关题目
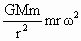 ,即
,即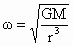
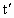 ,A、B转过的角度相差π的奇数倍时,则A、B相距最远,即:
,A、B转过的角度相差π的奇数倍时,则A、B相距最远,即: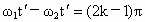 (k=1,2,3…)
(k=1,2,3…)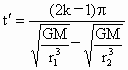 (k=1,2,3…)
(k=1,2,3…)
