Question

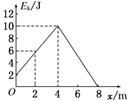
（10分） 质量m＝1 kg的物体，在水平拉力F(拉力方向与物体初速度方向相同) 的作用下，沿粗糙水平面运动，经过位移4 m时，拉力F停止作用，运动到位移是8 m时物体停止，运动过程中E_k－x的图线如图所示．求：(g取10 m/s²)

(1)物体的初速度多大？

(2)物体和平面间的动摩擦因数为多大？                                    

(3)拉力F的大小．

 

 

Answer 1

【答案】

(1)2 m/s　(2)0.25　(3)4.5 N

 (1)从图线可知初动能为2 J，

E_k0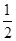＝mv²＝2 J，v＝2 m/s.                           （2分）

(2)在位移4 m处物体的动能为10 J，在位移8 m处物体的动能为零，这段过程中物体克

服摩擦力做功．

设摩擦力为F_f，则－F_fx₂＝0－10 J＝－10 J      F_f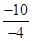＝ N＝2.5 N

因F_f＝μmg     故μ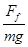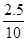＝＝＝0.25.                                  (4分)

(3)物体从开始到移动4 m这段过程中，受拉力F和摩擦力F_f的作用，合力为F－F_f，

根据动能定理有

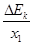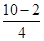(F－F_f)·x₁＝ΔE_k      故得F＝＋F_f＝(＋2.5) N＝4.5 N.                 (4分)

【解析】(1)从图线可知初动能为2 J，

E_k0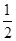＝mv²＝2 J，v＝2 m/s.                           （2分）

(2)在位移4 m处物体的动能为10 J，在位移8 m处物体的动能为零，这段过程中物体克

服摩擦力做功．

设摩擦力为F_f，则－F_fx₂＝0－10 J＝－10 J      F_f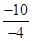＝ N＝2.5 N

因F_f＝μmg     故μ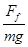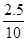＝＝＝0.25.                                  (4分)

(3)物体从开始到移动4 m这段过程中，受拉力F和摩擦力F_f的作用，合力为F－F_f，

根据动能定理有

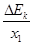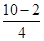(F－F_f)·x₁＝ΔE_k      故得F＝＋F_f＝(＋2.5) N＝4.5 N.                 (4分)

本题考查动能定理的应用，由图像可直接读出初动能为2J，由动能公式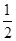mv²可求得此时速度大小，在位移4 m处物体的动能为10 J，在位移8 m处物体的动能为零，这段过程中物体克服摩擦力做功，由动能定理可求得克服阻力做功的大小，再由W=fs求得摩擦力大小，从而求得动摩擦因数的值，物体从开始到移动4 m这段过程中，受拉力F和摩擦力F_f的作用，根据动能定理可求得动能变化量及合外力做功，从而求得拉力大小