题目内容
18.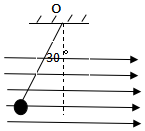 如图所示,一不可伸长的长为L的绝缘细线,一端固定于O点,另一端连着一个质量为m的带电小球带电量为q,在方向水平的匀强电场中处于静止状态,细线与竖直方向成30°角.求:
如图所示,一不可伸长的长为L的绝缘细线,一端固定于O点,另一端连着一个质量为m的带电小球带电量为q,在方向水平的匀强电场中处于静止状态,细线与竖直方向成30°角.求:(1)带点小球所带何种电荷;
(2)细线产生拉力大小多少;
(3)匀强电场的电场强度.
分析 (1)以小球为研究对象,分析受力情况,作出力图,根据电场强度方向,确定小球的电性;
(2)根据平衡条件,结合矢量的法则,及三角知识,即可求解拉力大小,
(3)依据电场力公式,求解电场强度的大小.
解答 解:(1)小球静止在该点,受力平衡,受到重力、电场力和绳子的拉力,电场力水平向左,与电场方向相反,说明小球带负电;
(2、3)小球受力分析,
由平衡条件得:T=$\frac{mg}{cos30°}$=$\frac{2\sqrt{3}}{3}mg$
且qE=mgtan30°
解得E=$\frac{\sqrt{3}mg}{3q}$;
答:(1)小球带负电;
(2)细线产生拉力大小$\frac{2\sqrt{3}}{3}mg$;
(3)匀强电场的电场强度$\frac{\sqrt{3}mg}{3q}$.
点评 本题考查了求电场强度、对绳子的拉力,掌握带电体在电场中平衡问题,理解力的矢量合成法则,及三角知识的运用,注意分析受力,作出力图是关键.

练习册系列答案
相关题目
8. 如图所示,一木块放在水平桌面上,在水平面内共受三个力,F1,F2和摩擦力,F1,F2在同一直线,物体沿水平面向右做匀速直线运动.其中F1=10N,F2=2N.若撤去力F1,物体继续向右运动,则以下说法正确的是( )
如图所示,一木块放在水平桌面上,在水平面内共受三个力,F1,F2和摩擦力,F1,F2在同一直线,物体沿水平面向右做匀速直线运动.其中F1=10N,F2=2N.若撤去力F1,物体继续向右运动,则以下说法正确的是( )
 如图所示,一木块放在水平桌面上,在水平面内共受三个力,F1,F2和摩擦力,F1,F2在同一直线,物体沿水平面向右做匀速直线运动.其中F1=10N,F2=2N.若撤去力F1,物体继续向右运动,则以下说法正确的是( )
如图所示,一木块放在水平桌面上,在水平面内共受三个力,F1,F2和摩擦力,F1,F2在同一直线,物体沿水平面向右做匀速直线运动.其中F1=10N,F2=2N.若撤去力F1,物体继续向右运动,则以下说法正确的是( )| A. | 木块所受合力为10N,方向水平向左 | |
| B. | 木块所受合力为6N,方向水平向右 | |
| C. | 木块所受摩擦力大小为2N,方向水平向左 | |
| D. | 木块所受摩擦力为8N,方向水平向左 |
9. 一含有理想变压器的电路如图所示,原线圈匝数为n1,副线圈匝数为n2,已知n1=2n2,图中电阻R1=R3=R4=R,R2=2R.U为正弦交流电压的有效值且恒定.则下列说法正确的是( )
一含有理想变压器的电路如图所示,原线圈匝数为n1,副线圈匝数为n2,已知n1=2n2,图中电阻R1=R3=R4=R,R2=2R.U为正弦交流电压的有效值且恒定.则下列说法正确的是( )
 一含有理想变压器的电路如图所示,原线圈匝数为n1,副线圈匝数为n2,已知n1=2n2,图中电阻R1=R3=R4=R,R2=2R.U为正弦交流电压的有效值且恒定.则下列说法正确的是( )
一含有理想变压器的电路如图所示,原线圈匝数为n1,副线圈匝数为n2,已知n1=2n2,图中电阻R1=R3=R4=R,R2=2R.U为正弦交流电压的有效值且恒定.则下列说法正确的是( )| A. | 电阻R1和R2上消耗的电功率的比值为2 | |
| B. | 电阻R1和R2上消耗的电功率的比值为3 | |
| C. | 副线圈两端的电压为$\frac{1}{4}$U | |
| D. | 副线圈两端的电压为$\frac{1}{3}$U |
6.某一质点做竖直上抛运动,在上升阶段的平均速度是5m/s,(g取10m/s2)则下列说法正确的是( )
| A. | 从抛出到落回抛出点所需时间为2s | B. | 从抛出到最高点所需时间为2s | ||
| C. | 上升的最大高度为5m | D. | 上升的最大高度为15m |
3.在“探究小车速度随时间变化的规律”实验中,其中的错误是( )
| A. | 将小车移到靠近长木板有滑轮的一端后,先接通电源,等打点稳定后,再释放小车 | |
| B. | 将打点计时器固定在长木板无滑轮一端,并接好电路 | |
| C. | 电磁打点计时器和电火花计时器中,电火花计时器的实验误差较小 | |
| D. | 电火花计时器在纸带上打点是靠振针和复写纸,电磁打点计时器在纸带上打点是靠电火花和墨粉 |
10.一遥控玩具小车在平直路上运动的位移-时间图象如图所示,则( )


| A. | 前15s内汽车行驶的路程为30 m | B. | 20 s末汽车的速度大小为1 m/s | ||
| C. | 前10 s内汽车的加速度为3 m/s2 | D. | 前25 s内汽车做单方向直线运动 |
7.关于质点的说法下列正确的是( )
| A. | 体积很小的物体一定可以看成质点 | |
| B. | 质量很大的物体一定不可以看成质点 | |
| C. | 研究巨轮在大海中所处的地理位置时,可以将巨轮看做质点 | |
| D. | 研究百米跑运动员的起跑动作时,可以将运动员看做质点 |
8. 某同学在研究电子在电场中的运动时,得到了电子由a点运动到b点的轨迹(图中实线所示),图中未标明方向的一组虚线可能是电场线,也可能是等势面,则下列说法正确的是( )
某同学在研究电子在电场中的运动时,得到了电子由a点运动到b点的轨迹(图中实线所示),图中未标明方向的一组虚线可能是电场线,也可能是等势面,则下列说法正确的是( )
 某同学在研究电子在电场中的运动时,得到了电子由a点运动到b点的轨迹(图中实线所示),图中未标明方向的一组虚线可能是电场线,也可能是等势面,则下列说法正确的是( )
某同学在研究电子在电场中的运动时,得到了电子由a点运动到b点的轨迹(图中实线所示),图中未标明方向的一组虚线可能是电场线,也可能是等势面,则下列说法正确的是( )| A. | 如果图中虚线是电场线,电子在a点动能较小 | |
| B. | 如果图中虚线是等势面,电子在a点动能较小 | |
| C. | 不论图中虚线是电场线还是等势面,都是电子在b点电势能小 | |
| D. | 不论图中虚线是电场线还是等势面,a点的电势都高于b点的电势 |
 如图所示,内壁光滑、半径为R的圆形轨道固定在竖直平面内,质量为m2的小球静止在轨道最低点,另一质量为m1的小球(两球均可视为质点)从左侧内壁与圆心O等高处由静止释放,第一次运动到最低点时与m2碰撞,碰后m2小球恰好能做完整的圆周运动,而m1小球沿右侧内壁上升的最大高度为$\frac{1}{2}$R.求:
如图所示,内壁光滑、半径为R的圆形轨道固定在竖直平面内,质量为m2的小球静止在轨道最低点,另一质量为m1的小球(两球均可视为质点)从左侧内壁与圆心O等高处由静止释放,第一次运动到最低点时与m2碰撞,碰后m2小球恰好能做完整的圆周运动,而m1小球沿右侧内壁上升的最大高度为$\frac{1}{2}$R.求: