题目内容
18. 如图所示,A、B为两上带电的平行金属板,板间形成匀强电扬,A、B两板间的电势差为U,两板间距为d,绝缘细线一端拴一质量为m的带电小球,另一端悬于O点.小球静止时,与A板相距$\frac{d}{3}$,细线与直方向的夹角为θ.求:
如图所示,A、B为两上带电的平行金属板,板间形成匀强电扬,A、B两板间的电势差为U,两板间距为d,绝缘细线一端拴一质量为m的带电小球,另一端悬于O点.小球静止时,与A板相距$\frac{d}{3}$,细线与直方向的夹角为θ.求:(1)球带何种电荷?电荷量多大?
(2)若将细线烧断,则小球做何种运动?它运动到A板需多少时间?
分析 (1)小球开始受重力、电场力和拉力处于平衡,从而判定电性,根据平衡条件求出带电小球的带电量..
(2)根据牛顿第二定律求出小球的加速度,结合小球的位移,通过位移时间公式求出小球运动的时间.
解答  解:(1)小球静止时,受三力:电场力qE、重力mg、线的拉力FT,如图所示.
解:(1)小球静止时,受三力:电场力qE、重力mg、线的拉力FT,如图所示.
由平衡条件可以判定,FT和重力mg、电场力qE的合力F是一对平衡力.球带正电;
由 q$\frac{U}{d}$=mgtanθ
得q=$\frac{mgdtanθ}{U}$
(2)小球开始受重力、电场力和拉力处于平衡,剪断细线后做匀加速直线运动.
由图可知,小球受到的合外力:F=$\frac{mg}{cosθ}$ ①
由牛顿第二定律得:a=$\frac{F}{m}$ …②
打到金属板上前,小球的位移:x=$\frac{\frac{d}{3}}{sinθ}$ …③
由运动公式有:x=$\frac{1}{2}$at2 …④
②③④联立解得:t=$\sqrt{\frac{2d}{3gtanθ}}$.
答:(1)小球将沿线向右下方做初速度为零的匀加速直线运动,直至打到右侧金属板上.
(2)小球剪断细线后做匀加速直线运动,经过$\sqrt{\frac{2d}{3gtanθ}}$到金属板上.
点评 本题考查了牛顿第二定律和运动学公式的综合,关键能够正确地受力分析,结合动力学知识求解,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
10.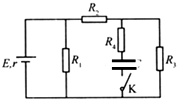 在如图所示的电路中,电源的电动势E=3.0V,内阻r=1.0Ω,电阻R1=10Ω,R2=10Ω,R3=30n,R4=35n;电容器的电容C=100μF.电容器原来不带电.则当接通开关K后流过R4的总电量为( )
在如图所示的电路中,电源的电动势E=3.0V,内阻r=1.0Ω,电阻R1=10Ω,R2=10Ω,R3=30n,R4=35n;电容器的电容C=100μF.电容器原来不带电.则当接通开关K后流过R4的总电量为( )
 在如图所示的电路中,电源的电动势E=3.0V,内阻r=1.0Ω,电阻R1=10Ω,R2=10Ω,R3=30n,R4=35n;电容器的电容C=100μF.电容器原来不带电.则当接通开关K后流过R4的总电量为( )
在如图所示的电路中,电源的电动势E=3.0V,内阻r=1.0Ω,电阻R1=10Ω,R2=10Ω,R3=30n,R4=35n;电容器的电容C=100μF.电容器原来不带电.则当接通开关K后流过R4的总电量为( )| A. | 2.0×10-4C | B. | 1.62×10-4C | C. | 2.0×10-4C | D. | 2.67×10-4C |
8. 如图所示,主动轮A通过皮带带动从动轮B按图示方向匀速转动,物体m随水平皮带匀速运动,则( )
如图所示,主动轮A通过皮带带动从动轮B按图示方向匀速转动,物体m随水平皮带匀速运动,则( )
 如图所示,主动轮A通过皮带带动从动轮B按图示方向匀速转动,物体m随水平皮带匀速运动,则( )
如图所示,主动轮A通过皮带带动从动轮B按图示方向匀速转动,物体m随水平皮带匀速运动,则( )| A. | 物体m受到向右的摩擦力 | |
| B. | 物体m不受摩擦力 | |
| C. | 主动轮上的P点所受摩擦力方向向上 | |
| D. | 从动轮上的Q点所受摩擦力方向向上 |

 由于下了大雪,许多同学在课间追逐嬉戏,尽情玩耍,而同学王清和张华却做了一个小实验:他们造出一个方形的雪块,让它以一定的初速度从一斜坡的底端沿坡面冲上该足够长的斜坡(坡上的雪已压实,斜坡表面平整),发现雪块能沿坡面最大上冲3.2m.已知雪块与坡面间的动摩擦因数为μ=0.05,他们又测量了斜坡的倾角为θ=37°,如图所示.他俩就估测出了雪块的初速度.那么:
由于下了大雪,许多同学在课间追逐嬉戏,尽情玩耍,而同学王清和张华却做了一个小实验:他们造出一个方形的雪块,让它以一定的初速度从一斜坡的底端沿坡面冲上该足够长的斜坡(坡上的雪已压实,斜坡表面平整),发现雪块能沿坡面最大上冲3.2m.已知雪块与坡面间的动摩擦因数为μ=0.05,他们又测量了斜坡的倾角为θ=37°,如图所示.他俩就估测出了雪块的初速度.那么: 利用图甲装置可以验证机械能守恒定律,实验中电火花计时器所用交流电源的频率为50Hz,得到如图乙所示的纸带.选取纸带上打出的连续五个点A、B、C、D、E,测出A点距起点O的距离为s0=19.00cm,点A、C间的距离为s1=8.36cm,点C、E间的距离为s2=9.88cm,g取9.8m/s2,测得重物的质量为100g.
利用图甲装置可以验证机械能守恒定律,实验中电火花计时器所用交流电源的频率为50Hz,得到如图乙所示的纸带.选取纸带上打出的连续五个点A、B、C、D、E,测出A点距起点O的距离为s0=19.00cm,点A、C间的距离为s1=8.36cm,点C、E间的距离为s2=9.88cm,g取9.8m/s2,测得重物的质量为100g.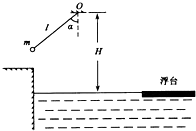 在游乐节目中,选手需要借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论.如图所示,他们将选手简化为质量m=60kg的指点,选手抓住绳由静止开始摆动,此事绳与竖直方向夹角α=30°,绳的悬挂点O距水面的高H=3m.不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深.取中立加速度g=10m/s2,sin53°=0.8,cos53°=0.6°
在游乐节目中,选手需要借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论.如图所示,他们将选手简化为质量m=60kg的指点,选手抓住绳由静止开始摆动,此事绳与竖直方向夹角α=30°,绳的悬挂点O距水面的高H=3m.不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深.取中立加速度g=10m/s2,sin53°=0.8,cos53°=0.6° 某些固体材料受到外力后除了产生形变,其电阻率也要发生变化,这种由于外力的作用而使材料电阻率发生变化的现象称为“压阻效应”.现用如图1所示的电路研究某长薄板电阻Rx的压阻效应,已知Rx的阻值变化范围为几欧到几十欧,实验室中有下列器材:
某些固体材料受到外力后除了产生形变,其电阻率也要发生变化,这种由于外力的作用而使材料电阻率发生变化的现象称为“压阻效应”.现用如图1所示的电路研究某长薄板电阻Rx的压阻效应,已知Rx的阻值变化范围为几欧到几十欧,实验室中有下列器材: 在匀强电场A.B.C三点的连线构成等腰三角形,α=45°,ϕA=10V,ϕB=2V.电场线与AB平行,C点的电势ϕc=6V.
在匀强电场A.B.C三点的连线构成等腰三角形,α=45°,ϕA=10V,ϕB=2V.电场线与AB平行,C点的电势ϕc=6V.