题目内容
9.如图所示,直角坐标系xOy位于竖直平面内,在x≤0的区域内有沿x轴负方向的匀强电场,在x>0的区域内有一方向垂直纸面向里、磁感应强度大小B=4.0×10-2T、宽度d=2m,边界垂直于x轴,位置待定的匀强磁场.一比荷为5.0×107C/kg的负粒子从P(-3,0)点以速度V0=2×106m/s沿y轴正方向射入电场,从y轴上的A(0,2$\sqrt{3}$)点射出匀强电场区域,再经匀强磁场偏转最终通过x轴上的Q(9,0)点(图中未标出),不计粒子重力.求:
(1)匀强电场的电场强度E:
(2)负粒子出电场时的速度v;
(3)匀强磁场区域的左边界的横坐标.
分析 (1)粒子在电场中做类平抛运动,根据牛顿第二定律和运动学公式求出电场强度的大小.
(2)根据平行四边形定则求出粒子射出电场时的速度大小和方向.
(3)作出粒子的运动轨迹,根据半径公式求出粒子在磁场中的运动半径,结合几何关系求出匀强磁场区域的左边界的横坐标.
解答 解:(1)负粒子垂直电场方向进入电场,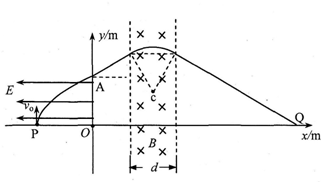
y=${v}_{0}t=2\sqrt{3}$ ①
x=$\frac{1}{2}a{t}^{2}=3$ ②
a=$\frac{qE}{m}$ ③
联立解得E=4×104N/C ④
(2)根据平行四边形定则知,v=$\sqrt{{{v}_{0}}^{2}+(at)^{2}}$,⑤
代入数据解得v=4×106m/s. ⑥
负粒子沿与x轴正方向成30°角的方向射出电场.
(3)负粒子进入磁场后做匀速圆周运动,根据牛顿第二定律有:
qvB=$m\frac{{v}^{2}}{r}$ ⑦
代入数据解得r=2m ⑧
轨迹如图所示,由几何关系得,C为粒子运动轨迹的圆心,且圆心角为60°,负粒子将沿x轴正方向成30°角方向射出磁场,则
tan60°=$\frac{9-(x+2)}{2\sqrt{3}+\frac{\sqrt{3}}{3}x}$ ⑨
解得x=0.5m.
答:(1)匀强电场的电场强度E为4×104N/C;
(2)负粒子出电场时的速度v为4×106m/s,沿与x轴正方向成30°角的方向射出电场;
(3)匀强磁场区域的左边界的横坐标为0.5m.
点评 本题考查了带电粒子在电场和磁场中的运动,掌握处理类平抛运动的方法,对于粒子在磁场中的运动,关键作出轨迹,结合半径公式和几何关系进行求解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
19.以下是有关近代物理内容的若干叙述,其中正确的是( )
| A. | 一束光照射到某种金属上不能发生光电效应,可能是因为这束光的光强太小 | |
| B. | 卢瑟福在a粒子散射实验的基础上提出原子核式结构学说 | |
| C. | 天然放射现象中发出的三种射线是从原子核内放出的看不见的射线 | |
| D. | 原子核发生一次β衰变,该原子外层就失去一个电子 | |
| E. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,但原子的能量增大 |
20.甲乙两队进行拔河比赛,甲队胜,若绳的质量不计,则( )
| A. | 甲队拉绳子的力大于乙队拉绳子的力 | |
| B. | 甲队与地面的最大静摩擦力大于乙队与地面的最大静摩擦力 | |
| C. | 甲乙两队与地面的最大静摩擦力大小相等,方向相反 | |
| D. | 甲乙两队拉绳的力大小相等 |
4.将一小球竖直向上抛出,小球到达最高点前的最后一秒内和离开最高点后的第一秒内通过的路程分别为xl和x2,速度变化量的大小分别为△v1和△v2,若小球所受空气阻力大小不变,则下列表述正确的是( )
| A. | x1>x2,△v1<△v2 | B. | x1<x2,△v1<△v2 | C. | x1>x2,△v1>△v2 | D. | x1<x2,△v1>△v2 |
14.关于电磁场和电磁波,下列说法不正确的是( )
| A. | 变化的电场能够产生磁场,变化的磁场能够产生电场 | |
| B. | 麦克斯韦第一次通过实验验证了电磁波的存在 | |
| C. | 无线电波、红外线、可见光、紫外线、x射线、γ射线都是电磁波 | |
| D. | 紫外线是一种波长比紫光更短的电磁波,能够灭菌消毒 |
1.下列说法中正确的是( )
| A. | 随着科学技术的发展,制冷机的制冷温度可以降到-280℃ | |
| B. | 随着科学技术的发展,热量可以从低温物体传到高温物体 | |
| C. | 随着科学技术的发展,热机的效率可以达到100% | |
| D. | 无论科技怎样发展,第二类永动机都不可能实现 | |
| E. | 无论科技怎样发展,都无法判断一温度升高的物体是通过做功还是热传递实现的 |
18. 如图所示的电路中,电源电动势为E,内阻为r,C为电容器,电流表A和电压表V均可视为理想电表.闭合开关S后,在将滑动变阻器的滑片P向右移动的过程中( )
如图所示的电路中,电源电动势为E,内阻为r,C为电容器,电流表A和电压表V均可视为理想电表.闭合开关S后,在将滑动变阻器的滑片P向右移动的过程中( )
 如图所示的电路中,电源电动势为E,内阻为r,C为电容器,电流表A和电压表V均可视为理想电表.闭合开关S后,在将滑动变阻器的滑片P向右移动的过程中( )
如图所示的电路中,电源电动势为E,内阻为r,C为电容器,电流表A和电压表V均可视为理想电表.闭合开关S后,在将滑动变阻器的滑片P向右移动的过程中( )| A. | 电流表A的示数变小,电压表V的示数变大 | |
| B. | 小灯泡L变暗 | |
| C. | 通过定值电阻R1的电流方向自右向左 | |
| D. | 电源的总功率变大,效率变小 |
19.下列说法正确的是( )
| A. | 由玻尔理论可知,氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能减小,电势能增大 | |
| B. | 对于同一种金属来说,其极限频率恒定,与入射光的频率及光的强度均无关 | |
| C. | 卢瑟福通过实验提出原子具有核式结构 | |
| D. | ${\;}_{90}^{234}Th$核发生β衰变时,新核与原来的原子核相比,中子数减少了l | |
| E. | 太阳内部发生的核反应是${\;}_{92}^{234}U$+${\;}_{0}^{1}n$→${\;}_{56}^{144}Ba$+${\;}_{36}^{89}Kr$+3${\;}_{0}^{1}n$ |
