题目内容
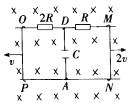
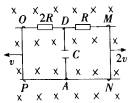
如图所示平面中,L1,L2是两根平行的直导线,MN和OP是垂直跨在L1,L2上并可左右滑动的两根平行直导线,每根的长度是L,在线路里接入了两个电阻和一个电容器(见图),电阻的阻值一个是R,另一个是2R,电容器的电容是C,把整个线路放在匀强磁场中,磁感应强度的大小为B,方向垂直纸面向里.当使MN以速率2v向右匀速滑动,而OP以速率v向左匀速滑动时,电容器的上极板的带电量等于多少?(除R,2R外其他电阻不计)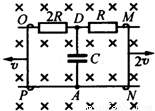
【答案】分析:导线L1,L2都做切割磁感线运动,产生感应电动势,由公式E=BLv求出两导线产生的感应电动势,由右手定则判断可知两个感应电动势串联,即可得到回路中总的感应电动势,再根据欧姆定律求出AD间的电压,即可由Q=CU求得电容器的电量.
解答:解:导线L1,L2做切割磁感线运动,产生感应电动势分别为:E1=BL?2v=2BLv,E2=BLv,
根据右手定则判断可知,两个感应电动势串联,回路中感应电流的方向沿逆时针,则回路中总的感应电动势为E=E1+E2=3BLv,
感应电流为 I=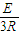 =
=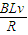
根据闭合电路欧姆定律得:DA间的电势差UDA=E1-IR=2BLv-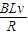 ?R=BLv
?R=BLv
故电容器的电量为Q=CU=CBLv,
由于上板的电势高,故上板带正电.
答:电容器的上极板的带电量等于CBLv.
点评:本题中双杆问题,注意判断两个感应电动势的关系,根据闭合电路欧姆定律求解电压时,可把R看成电源E1的内电阻或把2看成电源E2内电阻.
解答:解:导线L1,L2做切割磁感线运动,产生感应电动势分别为:E1=BL?2v=2BLv,E2=BLv,
根据右手定则判断可知,两个感应电动势串联,回路中感应电流的方向沿逆时针,则回路中总的感应电动势为E=E1+E2=3BLv,
感应电流为 I=
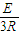 =
=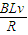
根据闭合电路欧姆定律得:DA间的电势差UDA=E1-IR=2BLv-
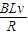 ?R=BLv
?R=BLv故电容器的电量为Q=CU=CBLv,
由于上板的电势高,故上板带正电.
答:电容器的上极板的带电量等于CBLv.
点评:本题中双杆问题,注意判断两个感应电动势的关系,根据闭合电路欧姆定律求解电压时,可把R看成电源E1的内电阻或把2看成电源E2内电阻.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示平面中,L1,L2是两根平行的直导线,MN和OP是垂直跨在L1,L2上并可左右滑动的两根平行直导线,每根的长度是L,在线路里接入了两个电阻和一个电容器(见图),电阻的阻值一个是R,另一个是2R,电容器的电容是C,把整个线路放在匀强磁场中,磁感应强度的大小为B,方向垂直纸面向里.当使MN以速率2v向右匀速滑动,而OP以速率v向左匀速滑动时,电容器的上极板的带电量等于多少?(除R,2R外其他电阻不计)
如图所示平面中,L1,L2是两根平行的直导线,MN和OP是垂直跨在L1,L2上并可左右滑动的两根平行直导线,每根的长度是L,在线路里接入了两个电阻和一个电容器(见图),电阻的阻值一个是R,另一个是2R,电容器的电容是C,把整个线路放在匀强磁场中,磁感应强度的大小为B,方向垂直纸面向里.当使MN以速率2v向右匀速滑动,而OP以速率v向左匀速滑动时,电容器的上极板的带电量等于多少?(除R,2R外其他电阻不计)