题目内容
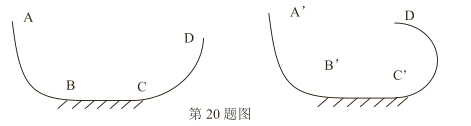
【题目】如图所示为一极限滑板运动的场地图，AB 和 CD 为一竖直平面光滑轨道，其中BC 水平，A 点高出 BC 5 米，CD 是半径为 R=4m 的 1/4 圆轨道，BC 长 2 米，一质量为 60千克的运动员（包含滑板）从 A 点静止滑下，经过 BC 后滑到高出 D 点 0.5 米位置速度为零。求：（
）
（1）滑板与 BC 轨道的滑动摩擦系数
（2）运动员第 3 次经过 C 点对轨道的压力
（3）现有另一下滑轨道， 
与 AB 轨道相同，CD 轨道换成半径
米的半圆轨道
，运动员从
轨道某位置静止滑下，则该运动员能否经
点落到
点，若能求出该位置，若不能说明理由。
【答案】（1）
（2）
(3)不存在.
【解析】（1）全过程由动能定理得： 
，即
解得： 
（2）从A到C由动能定理得： 
在C点，根据牛顿第二定律得： 
，
联立得： 
由牛顿第三定律得到： 
即人第三次经过C点时对轨道的压力为
（3）假设经过
点后平抛能够到达
，根据平抛运动的规律有：
， 
解得： 
，所以不存在
练习册系列答案
单元期中期末卷系列答案
相关题目
