题目内容
9. 如图所示,在倾角θ=37°的足够长的固定光滑斜面的底端,有一质量m=1.0kg、可视为质点的物体,以v0=6.0m/s的初速度沿斜面上滑.已知sin37°=0.60,cos37°=0.80,重力加速度g取10m/s2,不计空气阻力.求:
如图所示,在倾角θ=37°的足够长的固定光滑斜面的底端,有一质量m=1.0kg、可视为质点的物体,以v0=6.0m/s的初速度沿斜面上滑.已知sin37°=0.60,cos37°=0.80,重力加速度g取10m/s2,不计空气阻力.求:(1)物体的初动量和沿斜面向上运动的加速度大小;
(2)物体在沿斜面运动的过程中,物体克服重力所做功的最大值;
(3)物体在沿斜面向上运动至返回到斜面底端的过程中,重力的冲量.
分析 (1)根据动量的定义即可求得物体的初动量;根据牛顿第二定律进行分析,列式即可求得加速度;
(2)物体沿斜面上滑到最高点时,克服重力做功达到最大值,由动能定理进行分析,即可求出克服摩擦力所做的功;
(3)由运动学公式可求得滑行的总时间,再根据冲量的定义即可求得重力的冲量.
解答 解:(1)由动量的定义,可得物体的初动量为:
p0=m v0=1.0×6.0kgm/s=6.0kgm/s
设物体运动的加速度为a,物体所受合力等于重力沿斜面向下的分力为:
F=mgsinθ,
根据牛顿第二定律有:F=ma;
解得:a=6.0m/s2.
(2)物体沿斜面上滑到最高点时,克服重力做功达到最大值,设最大值为vm;
对于物体沿斜面上滑过程,根据动能定理有:
-W=0-$\frac{1}{2}$mvm2
解得:W=18J;
(3)物体沿斜面上滑和下滑的总时间为:
t=$\frac{2{v}_{0}}{a}$=$\frac{2×6}{6}$=2.0s
此过程中重力的冲量为:
I=mgt=10×2.0=20Ns
方向与重力方向相同,竖直向下.
答:(1)物体的初动量为6.0kgm/s;沿斜面向上运动的加速度大小为6.0m/s2.
(2)物体在沿斜面运动的过程中,物体克服重力所做功的最大值为18J;
(3)物体在沿斜面向上运动至返回到斜面底端的过程中,重力的冲量为20Ns,方向向下
点评 本题考查动能定理以及动量定理的应用,要注意明确动能定理中功和动能为标量,而动量定理中冲量和动量均为矢量,在应用动量定理时要注意方向性的掌握.

练习册系列答案
相关题目
20.下列说法中正确的是( )
| A. | 当一列声波从空气中传入水中时波长一定会变长 | |
| B. | 在机械横波传播方向上的某个质点的振动速度就是波的传播速度 | |
| C. | a、b两束光照射同一双缝干涉装置在屏上得到的干涉图样中,a光的相邻亮条纹间距小于b光的相邻亮条纹间距,则可以判断水对a光的折射率比b光大 | |
| D. | 电磁波是横波,可以观察到其偏振现象 |
4.下列现象中属于离心现象的是( )
| A. | 洗衣机把湿衣服甩干 | B. | 刹车时,乘客前倾 | ||
| C. | 从某一高度水平抛出一物体 | D. | 篮球运动员将篮球抛出 |
14. 如图所示,光滑杆AB与水平面间的夹角始终为θ,B端固定一根劲度系数为k、原长为l0的轻弹簧,质量为m的小球套在光滑杆上并与弹簧的上端连接,OO′为过B点的竖直轴,开始球处于静止状态.当球随杆一起绕OO′轴转动的角速度ω从0开始缓慢增大时,下列说法中正确的是( )
如图所示,光滑杆AB与水平面间的夹角始终为θ,B端固定一根劲度系数为k、原长为l0的轻弹簧,质量为m的小球套在光滑杆上并与弹簧的上端连接,OO′为过B点的竖直轴,开始球处于静止状态.当球随杆一起绕OO′轴转动的角速度ω从0开始缓慢增大时,下列说法中正确的是( )
 如图所示,光滑杆AB与水平面间的夹角始终为θ,B端固定一根劲度系数为k、原长为l0的轻弹簧,质量为m的小球套在光滑杆上并与弹簧的上端连接,OO′为过B点的竖直轴,开始球处于静止状态.当球随杆一起绕OO′轴转动的角速度ω从0开始缓慢增大时,下列说法中正确的是( )
如图所示,光滑杆AB与水平面间的夹角始终为θ,B端固定一根劲度系数为k、原长为l0的轻弹簧,质量为m的小球套在光滑杆上并与弹簧的上端连接,OO′为过B点的竖直轴,开始球处于静止状态.当球随杆一起绕OO′轴转动的角速度ω从0开始缓慢增大时,下列说法中正确的是( )| A. | 小球静止时,弹簧的压缩量为$\frac{mgsinθ}{k}$ | |
| B. | 当ω=$\sqrt{\frac{2gsinθ}{{l}_{0}co{s}^{2}θ}}$时,弹簧处于原长状态 | |
| C. | 小球从静止到弹簧处于原长状态的过程中,合外力做的功为$\frac{1}{2}$mgl0sinθ | |
| D. | 小球从静止到弹簧处于原长状态的过程中,重力势能增加了$\frac{{m}^{2}{g}^{2}sinθ}{k}$ |
1.下列说法中符合开普勒对行星绕太阳运动的描述是( )
| A. | 所有的行星都在同一椭圆轨道上绕太阳运动 | |
| B. | 行星绕太阳运动时,太阳在椭圆的一个焦点上 | |
| C. | 行星从近日点向远日点运动时,速率逐渐增大 | |
| D. | 离太阳越远的行星,公转周期越短 |
18. 如图所示,电容器与电动势为E的直流电源(内阻不计)连接,下极板接地.一带电油滴位于电容器中的P点恰好处于静止状态.现将平行板电容器的上极板竖直向下移动一小段距离,则( )
如图所示,电容器与电动势为E的直流电源(内阻不计)连接,下极板接地.一带电油滴位于电容器中的P点恰好处于静止状态.现将平行板电容器的上极板竖直向下移动一小段距离,则( )
 如图所示,电容器与电动势为E的直流电源(内阻不计)连接,下极板接地.一带电油滴位于电容器中的P点恰好处于静止状态.现将平行板电容器的上极板竖直向下移动一小段距离,则( )
如图所示,电容器与电动势为E的直流电源(内阻不计)连接,下极板接地.一带电油滴位于电容器中的P点恰好处于静止状态.现将平行板电容器的上极板竖直向下移动一小段距离,则( )| A. | P点的电势将降低 | B. | 电容器极板所带电荷量减小 | ||
| C. | 带电油滴的电势能将减小 | D. | 带电油滴仍处于静止状态 |
 如图所示,质量均为m=1kg的A、B两物体通过劲度系数为k=100N/m的轻质弹簧拴接在一起,物体A处于静止状态.在A的正上方h高处有一质量为$\frac{m}{2}$的小球C,由静止释放,当C与A发生弹性碰撞后立刻取走小球C,h至少多大,碰后物体B有可能被拉离地面?
如图所示,质量均为m=1kg的A、B两物体通过劲度系数为k=100N/m的轻质弹簧拴接在一起,物体A处于静止状态.在A的正上方h高处有一质量为$\frac{m}{2}$的小球C,由静止释放,当C与A发生弹性碰撞后立刻取走小球C,h至少多大,碰后物体B有可能被拉离地面?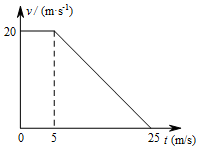 一辆客车正在以v1=20m/s的速度匀速行驶,突然,司机看见正前方x=65m(距车队队尾)处有一列汽车车队以8m/s的速度正在匀速行驶,相邻汽车间距为20m,客车司机立即采取制动措施.若从司机看见车队开始计时(t=0),客车的速度-时间图象如图所示(汽车和客车大小不计).
一辆客车正在以v1=20m/s的速度匀速行驶,突然,司机看见正前方x=65m(距车队队尾)处有一列汽车车队以8m/s的速度正在匀速行驶,相邻汽车间距为20m,客车司机立即采取制动措施.若从司机看见车队开始计时(t=0),客车的速度-时间图象如图所示(汽车和客车大小不计).