题目内容
如图所示，球重为G，半径为R，紧靠在竖直墙上，木块重为W，厚为h，放在球边，当对木块施以水平推力F后，球刚好对地面压力为零，如不计一切摩擦，
求：（1）F的大小；
（2）木块对地面的压力．
求：（1）F的大小；
（2）木块对地面的压力．
对球进行受力分析如图：
由三角形相似可得：sinθ=
由平衡条件得：F′=G
sinθ=
=
，
解得：F1=
对木块受力分析并正交分解如图：
由平衡条件得：
水平方向：F=cosθ，即：F=
×
=
竖直方向：N=W+F1sinθ=W+
×
=W+G
由牛顿第三定律得：
木块对地面的压力为：W+G
答：（1）F的大小为：
（2）木块对地面的压力为：W+G
由三角形相似可得：sinθ=
| R-h |
| R |
由平衡条件得：F′=G
sinθ=
| G |
| F1 |
| R-h |
| R |
解得：F1=
| GR |
| R-h |
对木块受力分析并正交分解如图：
由平衡条件得：
水平方向：F=cosθ，即：F=
| GR |
| R-h |
| ||
| R |
G
| ||
| R-h |
竖直方向：N=W+F1sinθ=W+
| GR |
| R-h |
| R-h |
| R |
由牛顿第三定律得：
木块对地面的压力为：W+G
答：（1）F的大小为：
G
| ||
| R-h |
（2）木块对地面的压力为：W+G
练习册系列答案
相关题目
如图所示，球重为G，半径为R，紧靠在竖直墙上，木块重为W，厚为h，放在球边，当对木块施以水平推力F后，球刚好对地面压力为零，如不计一切摩擦，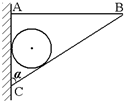
如图所示，球重为G，半径为R，由轻杆BC支持并靠在墙上，轻杆长为L，C端铰于墙上，B端用水平绳拉住，系于墙上A处，杆与墙的夹角为α．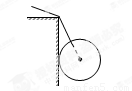
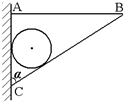如图所示，球重为G，半径为R，由轻杆BC支持并靠在墙上，轻杆长为L，C端铰于墙上，B端用水平绳拉住，系于墙上A处，杆与墙的夹角为α．
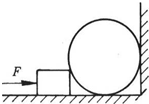如图所示，球重为G，半径为R，紧靠在竖直墙上，木块重为W，厚为h，放在球边，当对木块施以水平推力F后，球刚好对地面压力为零，如不计一切摩擦，