题目内容
13.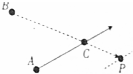 如图所示为两个足球运动员练习助攻进球的过程,其中BP在一条直线上,假设甲运动员在B处将足球以10m/s的速度沿直线BP的方向踢出,足球沿着地面向P处运动,足球运动的加速度大小为1m/s2,在A位置的乙运动员发现甲运动员将足球踢出去后,经过1s的反应时间后,开始匀加速向BP连线上的C处奔去,乙运动员的最大速度为8m/s,已知B、C两点间的距离为50m,A、C两点间的距离为56m.
如图所示为两个足球运动员练习助攻进球的过程,其中BP在一条直线上,假设甲运动员在B处将足球以10m/s的速度沿直线BP的方向踢出,足球沿着地面向P处运动,足球运动的加速度大小为1m/s2,在A位置的乙运动员发现甲运动员将足球踢出去后,经过1s的反应时间后,开始匀加速向BP连线上的C处奔去,乙运动员的最大速度为8m/s,已知B、C两点间的距离为50m,A、C两点间的距离为56m.(1)乙运动员以多大的加速度做匀加速运动,才能与足球同时运动到C位置?
(2)乙运动员运动到C处后以一定的速度将足球沿CP方向踢出,已知足球从C向P做匀减速运动,足球运动的加速度大小仍然为1m/s2,假设C点到P点的距离为9.5m,守门员看到运动员在C处将足球沿CP方向踢出后,能够到达P处扑球的时间为1s,那么乙运动员在C处给足球的速度至少多大,足球才能射进球门?
分析 (1)足球做匀减速直线运动,运动员做匀加速直线运动,应用匀变速直线运动规律可以求出运动员的加速度.
(2)足球做匀减速直线运动,已知位移、加速度、运动时间,应用位移公式可以求出初速度.
解答 解:(1)对足球:BC=v0t-$\frac{1}{2}$at2,即:50=10t-$\frac{1}{2}$×1×t2,解得:t=10s,
乙运动员的运动时间:t乙=t-1=9s,
乙运动员的最大速度为8m/s,乙运动员应先加速后匀速到达C处,设加速的时间为t′,则位移:AC=$\frac{{v}_{乙最大}}{2}$t′+v乙最大(t乙-t′),
即:56=$\frac{8}{2}$×t′+8×(9-t′),
解得:t′=4s,
乙加速结束的速度:v乙最大=a乙t′,
解得:a乙=$\frac{{v}_{乙最大}}{t′}$=$\frac{8}{4}$=2m/s2;
(2)由题意可知,足球从C到P的运动时间为1s,足球的位移:CP=vt-$\frac{1}{2}$at2,
即:9.5=v×1-$\frac{1}{2}$×1×12,
解得:v=10m/s;
答:(1)乙运动员以2m/s2的加速度做匀加速运动,才能与足球同时运动到C位置.
(2)乙运动员在C处给足球的速度至少为10m/s,足球才能射进球门.
点评 本题考查了求加速度与速度问题,分析清楚各研究对象的运动过程与运动性质,应用匀变速直线运动的运动规律即可正确解题.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
3. 一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数($\frac{1}{v}$)图象如图所示.若已知汽车的质量,则根据图象所给的信息,下列说法正确的是( )
一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数($\frac{1}{v}$)图象如图所示.若已知汽车的质量,则根据图象所给的信息,下列说法正确的是( )
 一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数($\frac{1}{v}$)图象如图所示.若已知汽车的质量,则根据图象所给的信息,下列说法正确的是( )
一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数($\frac{1}{v}$)图象如图所示.若已知汽车的质量,则根据图象所给的信息,下列说法正确的是( )| A. | 汽车一直做匀加速运动 | |
| B. | 汽车行驶的最大速度为20m/s | |
| C. | 发动机牵引力对汽车做的功等于汽车机械能的增加 | |
| D. | 能求出汽车运动到最大速度所需的时间 |
18.下列说法不正确的是( )
| A. | 只有横波才能产生干涉现象和多普勒效应 | |
| B. | 均匀变化的磁场产生均匀变化的电场向外传播就形成了电磁波 | |
| C. | 泊松亮斑支持了光的波动说,而光电效应支持了光的粒子说 | |
| D. | 由红光和绿光组成的一细光束从水中射向空气,在不断增大入射角时水面上首先消失的是绿光 |
2.如图甲,两水平金属板间距为d,板间电场强度的变化规律如图乙所示.t=0时刻,质量为m的带电微粒以初速度为v0沿中线射入两板间,0~$\frac{T}{3}$时间内微粒匀速运动,T时刻微粒恰好经金属板边缘飞出.微粒运动过程中未与金属板接触.重力加速度的大小为g.关于微粒在0~T时间内运动的描述,正确的是( )


| A. | 末速度大小为$\sqrt{2}$v0 | B. | 末速度沿水平方向 | ||
| C. | 重力势能减少了$\frac{1}{2}$mgd | D. | 克服电场力做功为mgd |
 某电场的等势面如图所示,若单位正电荷q=1C沿任一路径从点A移到B点,静电力所做的功是0J.从A点移到C点,静电力所做的功是4J.从B点移到C点,静电力所做的功是4J.则WAC等于WBC.(选填“大于”、“等于”、“小于”)
某电场的等势面如图所示,若单位正电荷q=1C沿任一路径从点A移到B点,静电力所做的功是0J.从A点移到C点,静电力所做的功是4J.从B点移到C点,静电力所做的功是4J.则WAC等于WBC.(选填“大于”、“等于”、“小于”) 如图所示,一根长l=75cm、一端封闭的粗细均匀的玻璃管,管内有一段长h=25cm的水银柱,当玻璃管开口向上竖直放置时,管内水银柱封闭气柱的长度l1=36cm.已知外界大气压强p=75cmHg,管内、外气体的温度不变.如果将玻璃管倒置,使开口竖直向下,问水银柱长度将是多少厘米?
如图所示,一根长l=75cm、一端封闭的粗细均匀的玻璃管,管内有一段长h=25cm的水银柱,当玻璃管开口向上竖直放置时,管内水银柱封闭气柱的长度l1=36cm.已知外界大气压强p=75cmHg,管内、外气体的温度不变.如果将玻璃管倒置,使开口竖直向下,问水银柱长度将是多少厘米? 如图所示,有一光滑的半圆形绝缘轨道QPN竖直放置与一水平绝缘轨道MN相切连接,轨道半径R=20cm,MN长x=60cm,在MN的右侧连接一光滑斜面,斜面倾角θ=37°,在轨道上M点左侧存在E=1×103N/C的竖直匀强电场,场强方向向下.一带负电、电荷量q=10-4C的小滑块质量m=20g,与水平轨道间的动摩擦因数μ=0.5,从斜面上某处静止滑下,(滑块经过M点时无能量损失),取重力加速度g=10m/s2.求:
如图所示,有一光滑的半圆形绝缘轨道QPN竖直放置与一水平绝缘轨道MN相切连接,轨道半径R=20cm,MN长x=60cm,在MN的右侧连接一光滑斜面,斜面倾角θ=37°,在轨道上M点左侧存在E=1×103N/C的竖直匀强电场,场强方向向下.一带负电、电荷量q=10-4C的小滑块质量m=20g,与水平轨道间的动摩擦因数μ=0.5,从斜面上某处静止滑下,(滑块经过M点时无能量损失),取重力加速度g=10m/s2.求: 如图所示,“凸”字形硬质金属线框质量为m,相邻各边相互垂直,且处于同一竖直平面内,ab边长为l,cd边长为2l,ab与cd平行,间距为2l.匀强磁场区域的上下边界均水平,磁场方向垂直于线框所在平面.开始时,cd边到磁场上边界的距离为2l,线框由静止释放,从cd边进入磁场直到ef、pq边进入磁场前,线框做匀速运动.在ef、pq边离开磁场后,ab边离开磁场之前,线框又做匀速运动.线框完全穿过磁场过程中产生的热量为Q.线框在下落过程中始终处于原竖直平面内,且ab、cd边保持水平,重力加速度为g.求:
如图所示,“凸”字形硬质金属线框质量为m,相邻各边相互垂直,且处于同一竖直平面内,ab边长为l,cd边长为2l,ab与cd平行,间距为2l.匀强磁场区域的上下边界均水平,磁场方向垂直于线框所在平面.开始时,cd边到磁场上边界的距离为2l,线框由静止释放,从cd边进入磁场直到ef、pq边进入磁场前,线框做匀速运动.在ef、pq边离开磁场后,ab边离开磁场之前,线框又做匀速运动.线框完全穿过磁场过程中产生的热量为Q.线框在下落过程中始终处于原竖直平面内,且ab、cd边保持水平,重力加速度为g.求: