题目内容
1. 在做“研究平抛运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.
在做“研究平抛运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽轨道的末端调整水平,在一块平整的木板表面钉上白纸和复写纸.将该木板竖直立于水平地面上,使小球从斜槽上紧靠挡板处由静止释放,小球撞到木板并在白纸上留下痕迹A;将木板向远离槽口平移距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞在木板上得到痕迹B;又将木板再向远离槽口平移距离x,小球再从斜槽上紧靠挡板处由静止释放,再得到痕迹C.若测得木板每次移动距离x=10.00cm,A、B间距离y1=5.02cm,B、C间距离y2=14.82cm.请回答以下问题(g=9.80m/s2)
(1)为什么每次都要使小球从斜槽上同一位置紧靠挡板处由静止释放?为了保证小球每次做平抛运动的初速度相同.
(2)根据以上直接测量的物理量来求得小球初速度的表达式为v0=x$\sqrt{\frac{g}{{y}_{2}-{y}_{1}}}$.(用题中所给字母表示)
(3)小球初速度的值为v0=1.00 m/s.
分析 明确实验的注意事项,根据平抛运动规律在水平和竖直方向的规律,尤其是在竖直方向上,连续相等时间内的位移差为常数,列出方程即可正确求解.
解答 解:(1)该实验中,为了确保小球每次抛出的轨迹相同,应该使抛出时的初速度相同,因此每次都应使小球从斜槽上紧靠档板处由静止释放.
(2)在竖直方向上:$△y={y}_{2}-{y}_{1}=g{t}^{2}$
水平方向上:x=v0t
联立方程解得:v0=x$\sqrt{\frac{g}{{y}_{2}-{y}_{1}}}$.
(3)根据:v0=x$\sqrt{\frac{g}{{y}_{2}-{y}_{1}}}$.
代入数据解得:v0=1.00m/s
故答案为:(1)为了保证小球每次做平抛运动的初速度相同
(2)x$\sqrt{\frac{g}{{y}_{2}-{y}_{1}}}$
(3)1.00.
点评 本题主要考查了匀变速直线运动中基本规律以及推论的应用,平时要加强练习,提高应用基本规律解决问题能力.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
11.分别用长为L的细线和轻杆拉一物体在竖直面内做圆周运动,设小球到达最高点时的速度分别为v1和v2,则( )
| A. | v1≥0,v2≥$\sqrt{gL}$ | B. | v1≥$\sqrt{gL}$,v2≥0 | C. | 0≤v1≤$\sqrt{gL}$,v2≥0 | D. | v1=v2=0 |
10. 如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
 如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )| A. | Bmin=$\frac{2m{v}_{0}}{qa}$,t=$\frac{7πa}{6v}$ | B. | Bmin=$\frac{6m{v}_{0}}{qa}$,t=$\frac{7πa}{6v}$ | ||
| C. | Bmin=$\frac{2m{v}_{0}}{qa}$,t=$\frac{πa}{26v}$ | D. | Bmin=$\frac{6m{v}_{0}}{qa}$,t=$\frac{πa}{26v}$ |
 某兴趣小组对一辆自制小遥控车的性能进行研究.他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2~10s时间段内的图象为曲线外,其余时间段图象均为直线).已知小车运动的过程中,2~14s时间段内小车的功率保持不变,在14s末失去动力小车自由滑行.已知小车的质量为1kg,整个过程中小车所受到的阻力大小恒定.求小车加速运动过程中行驶的距离.
某兴趣小组对一辆自制小遥控车的性能进行研究.他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2~10s时间段内的图象为曲线外,其余时间段图象均为直线).已知小车运动的过程中,2~14s时间段内小车的功率保持不变,在14s末失去动力小车自由滑行.已知小车的质量为1kg,整个过程中小车所受到的阻力大小恒定.求小车加速运动过程中行驶的距离. 如图甲所示,在同一竖直平面内的两正对着的相同半圆光滑轨道,相隔一定的距离,虚线沿竖直方向,一小球能在其间运动,今在最高点A与最低点B各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来,当轨道距离变化时,测得两点压力差与距离x的图象如图乙所示,g取10m/s2,不计空气阻力.求:
如图甲所示,在同一竖直平面内的两正对着的相同半圆光滑轨道,相隔一定的距离,虚线沿竖直方向,一小球能在其间运动,今在最高点A与最低点B各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来,当轨道距离变化时,测得两点压力差与距离x的图象如图乙所示,g取10m/s2,不计空气阻力.求: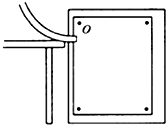 (1)“探究平抛物体的运动规律”实验的装置如图所示,让小球多次沿同一轨道运动,通过描点法画小球做平抛运动的轨迹.为了能较准确地描绘运动轨迹,下面列出了一些操作要求,将你认为正确的选项前面的字母填在横线上:ACE.
(1)“探究平抛物体的运动规律”实验的装置如图所示,让小球多次沿同一轨道运动,通过描点法画小球做平抛运动的轨迹.为了能较准确地描绘运动轨迹,下面列出了一些操作要求,将你认为正确的选项前面的字母填在横线上:ACE. 光的“逆向反射”又称再归反射,俗称后反射,它和我们熟知的镜面反射、漫反射不同,能使光线沿原来的路径反射回去,该现象在交通上有很广泛的应用,在山区盘山公路的路面上一般都等间距地镶嵌一些玻璃球,当夜间行驶的汽车车灯照上后显得非常醒目,以提醒司机注意.若小玻璃球的半径为R,折射率为1.73,如图所示,今有一束平行光沿直径AB方向照在小玻璃球上,试求离AB多远的入射光经折射-反射-折射再射出后沿原方向返回,即实现“逆向反射”.
光的“逆向反射”又称再归反射,俗称后反射,它和我们熟知的镜面反射、漫反射不同,能使光线沿原来的路径反射回去,该现象在交通上有很广泛的应用,在山区盘山公路的路面上一般都等间距地镶嵌一些玻璃球,当夜间行驶的汽车车灯照上后显得非常醒目,以提醒司机注意.若小玻璃球的半径为R,折射率为1.73,如图所示,今有一束平行光沿直径AB方向照在小玻璃球上,试求离AB多远的入射光经折射-反射-折射再射出后沿原方向返回,即实现“逆向反射”.