题目内容
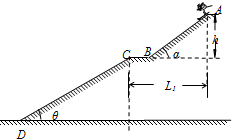
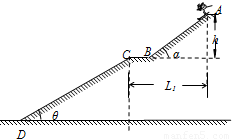
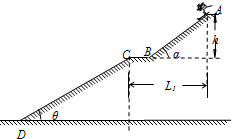 如图为某高台滑雪轨道部分简化示意图.其中AB段是助滑雪道,倾角为α,BC段是水平起跳台,CD段是着陆雪道,倾角θ=37°,轨道各部分与滑雪板间的动摩擦因数均为μ=0.25,图中轨道最高点A处的起滑台距起跳台BC的竖直高度h=10m.A点与C点的水平距离L1=20m,C点与D点的距离为DC=28.125m,运动员连同滑雪板的质量m=60kg.滑雪运动员从A点由静止开始起滑,通过起跳台从C点水平飞出,在落到着陆雪道上时,运动员靠改变姿势自己的速度全部转化成沿着斜面方向,且无能量损失.运动员均可视为质点,设运动员在全过程中不使用雪杖助滑,忽略空气阻力的影响,取重力加速度g=10m/s2,求:
如图为某高台滑雪轨道部分简化示意图.其中AB段是助滑雪道,倾角为α,BC段是水平起跳台,CD段是着陆雪道,倾角θ=37°,轨道各部分与滑雪板间的动摩擦因数均为μ=0.25,图中轨道最高点A处的起滑台距起跳台BC的竖直高度h=10m.A点与C点的水平距离L1=20m,C点与D点的距离为DC=28.125m,运动员连同滑雪板的质量m=60kg.滑雪运动员从A点由静止开始起滑,通过起跳台从C点水平飞出,在落到着陆雪道上时,运动员靠改变姿势自己的速度全部转化成沿着斜面方向,且无能量损失.运动员均可视为质点,设运动员在全过程中不使用雪杖助滑,忽略空气阻力的影响,取重力加速度g=10m/s2,求:(1)从C点水平飞出时速度的大小;
(2)运动员在着陆雪道CD上的着陆位置与C点的距离;
(3)运动员滑过D点时的速度大小;
(4)滑雪运动员从A到D克服摩擦力做的功为多少.
分析:(1)把运动员连同滑雪板看成一个质点,从A运动到C的过程中运用动能定理即可求出到达C点速度;
(2)运动员从C点水平飞出后做平抛运动,最后落在CD上,竖直方向的位移和水平方向位移比是个定值,根据平抛运动的规律即可解题;
(3)先求解运动到着陆雪道的初速度,然后再根据牛顿第二定律求解加速度,并根据运动学公式求解末速度;
(4)对A到D整个过程运用动能定理列式求解.
(2)运动员从C点水平飞出后做平抛运动,最后落在CD上,竖直方向的位移和水平方向位移比是个定值,根据平抛运动的规律即可解题;
(3)先求解运动到着陆雪道的初速度,然后再根据牛顿第二定律求解加速度,并根据运动学公式求解末速度;
(4)对A到D整个过程运用动能定理列式求解.
解答:解:(1)滑雪运动员从A到C的过程中,由动能定理得:
mgh-μmgL=
mvc2-0
解得vc=10m/s
(2)滑雪运动员从C水平飞出落到着陆雪道过程中做平抛运动,
x=vct…①
y=
gt2…②
tgθ=
…③
得 t=1.5s,x=15m;
着陆点位置与C点的距离s=
解得s=18.75m;
着陆位置到D点的距离s’=DC-S=9.375m
(3)滑雪运动员在着陆雪道上做匀加速直线运动
初速度为v0=
=
根据牛顿第二定律,有:mgsinθ-μmgcosθ=ma1
解得a1=4m/s2
运动到D点的速度设为vD,根据运动学公式,有vD2-v02=2a1s’
解得vD=20m/s
(4)从A点到D点动能定理mg(h+CDsinθ)-Wf=
m
-0
Wf=4125J
答:(1)从C点水平飞出时速度的大小为10m/s;
(2)运动员在着陆雪道CD上的着陆位置到C点的距离为18.75m;
(3)运动员滑过D点时的速度大小为20m/s;
(4)滑雪运动员从A到D克服摩擦力做的功为为4125J.
mgh-μmgL=
| 1 |
| 2 |
解得vc=10m/s
(2)滑雪运动员从C水平飞出落到着陆雪道过程中做平抛运动,
x=vct…①
y=
| 1 |
| 2 |
tgθ=
| y |
| x |
得 t=1.5s,x=15m;
着陆点位置与C点的距离s=
| x |
| cosθ |
解得s=18.75m;
着陆位置到D点的距离s’=DC-S=9.375m
(3)滑雪运动员在着陆雪道上做匀加速直线运动
初速度为v0=
|
| 325 |
根据牛顿第二定律,有:mgsinθ-μmgcosθ=ma1
解得a1=4m/s2
运动到D点的速度设为vD,根据运动学公式,有vD2-v02=2a1s’
解得vD=20m/s
(4)从A点到D点动能定理mg(h+CDsinθ)-Wf=
| 1 |
| 2 |
| v | 2 D |
Wf=4125J
答:(1)从C点水平飞出时速度的大小为10m/s;
(2)运动员在着陆雪道CD上的着陆位置到C点的距离为18.75m;
(3)运动员滑过D点时的速度大小为20m/s;
(4)滑雪运动员从A到D克服摩擦力做的功为为4125J.
点评:本题关键明确运动员的运动性质,然后分段运用平抛运动规律、牛顿第二定律、动能定理、运动学公式列式求解.

练习册系列答案
相关题目
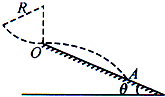 如图所示,是某跳台滑雪的雪道示意简化图,高台滑雪运动员经过一段竖直平面内的圆弧后,从圆弧所在圆的最低点O水平飞出,圆弧半径R=10m.一滑雪运动员连同滑雪板的总质量为50kg,从圆弧轨道上距O点竖直高度为3R/5处静止下滑,经过圆弧上的O点时受到的支持力大小为1000N,飞出后经时间t=2s着陆在雪道上的A点.忽略空气阻力,取重力加速度g=10m/s2.求:
如图所示,是某跳台滑雪的雪道示意简化图,高台滑雪运动员经过一段竖直平面内的圆弧后,从圆弧所在圆的最低点O水平飞出,圆弧半径R=10m.一滑雪运动员连同滑雪板的总质量为50kg,从圆弧轨道上距O点竖直高度为3R/5处静止下滑,经过圆弧上的O点时受到的支持力大小为1000N,飞出后经时间t=2s着陆在雪道上的A点.忽略空气阻力,取重力加速度g=10m/s2.求: