题目内容
 如图所示,一转盘可绕其竖直轴在水平面内转动,转动半径为R,在转台边缘放一物块A,当转台的角速度为ω0时,物块刚能被甩出转盘.若在物块A与转轴中心O连线中点再放一与A完全相同的物块B(A、B均可视为质点),并用细线相连接.当转动角速度ω为多大时,两物块将开始滑动?
如图所示,一转盘可绕其竖直轴在水平面内转动,转动半径为R,在转台边缘放一物块A,当转台的角速度为ω0时,物块刚能被甩出转盘.若在物块A与转轴中心O连线中点再放一与A完全相同的物块B(A、B均可视为质点),并用细线相连接.当转动角速度ω为多大时,两物块将开始滑动?分析:先根据当转台的角速度为ω0时,物块A刚能被甩出转盘,求出最大静摩擦力,当两物块将开始滑动时,两物体受到的摩擦力都为最大静摩擦力,分别对AB运用向心力公式联立即可求解.
解答:解:设两物体质量为m,圆盘半径为r,最大静摩擦力为fm,
则fm=mω02r
设马上要滑动时绳的拉力为T,此时两物体受到的摩擦力都为最大静摩擦力,对A有
T+fm=mω2r
对B有 fm-T=mω2?
联立解得:ω=
ω0
答:当转动角速度ω为
ω0 时,两物块将开始滑动.
则fm=mω02r
设马上要滑动时绳的拉力为T,此时两物体受到的摩擦力都为最大静摩擦力,对A有
T+fm=mω2r
对B有 fm-T=mω2?
| r |
| 2 |
联立解得:ω=
2
| ||
| 3 |
答:当转动角速度ω为
2
| ||
| 3 |
点评:本题的关键是抓住临界状态,隔离物体,正确受力分析,运用向心力公式求解,难度适中.

练习册系列答案
相关题目
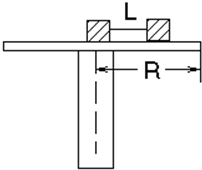 如图所示,一圆盘可以绕其竖直轴在水平面内运动,圆盘半径为R,甲、乙两物体的质量分别为M和m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用长为L的轻绳连在一起,L<R.若将甲物体放在转轴位置上,甲、乙连线正好沿半径方向拉直,开始时转盘角速度为零且连线无张且甲、乙物体均可视为质点.现缓慢增大转盘的角速度ω,试求:
如图所示,一圆盘可以绕其竖直轴在水平面内运动,圆盘半径为R,甲、乙两物体的质量分别为M和m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用长为L的轻绳连在一起,L<R.若将甲物体放在转轴位置上,甲、乙连线正好沿半径方向拉直,开始时转盘角速度为零且连线无张且甲、乙物体均可视为质点.现缓慢增大转盘的角速度ω,试求:

