题目内容
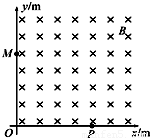
如图所示,在第一象限区域内有垂直于纸面向里的匀强磁场,磁感应强度大小B=2.0×10-3T,一带正电荷的粒子A以v=3.5×104m/s的速率从x轴上的P(0.50,0)处以与x轴正方向成某一角度的方向垂直射入磁场,从y轴上的M(0,0.50)处射出磁场,且运动轨迹的半径是所有可能半径值中的最小值.设粒子A的质量为m、电荷量为q.不计粒子的重力.
(1)求粒子A的比荷
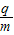 ;(计算结果请保留两位有效数字,下同)
;(计算结果请保留两位有效数字,下同)(2)如果粒子A运动过程中的某个时刻,在第一象限内再加一个匀强电场,就可以使其此后沿x轴负方向做匀速直线运动并离开第一象限,求该匀强电场的场强大小和方向,并求出粒子射出磁场处的坐标值;
(3)如果要粒子A按题干要求从M处射出磁场,第一象限内的磁场可以局限在一个最小的矩形区域内,求出这个最小的矩形区域的面积.
【答案】分析:(1)考查带电粒子在磁场中的运动,根据粒子的运动的轨迹可以求得粒子的比荷.
(2)粒子做的是匀速直线运动,所以粒子处于受力平衡状态,由此可以求得电场的大小和方向.
(3)是带电粒子在有界磁场(矩形区域)中的运动,当磁场和带电粒子的轨迹相切时,磁场的面积最小
解答:解: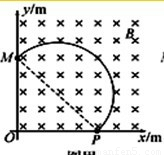
(1)该粒子在磁场中运动半径为r,如图甲,依题意MP连线即为该粒子在磁场中做匀速圆周运动的最小直径,由几何关系得:
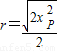 =
=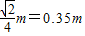 ①
①
粒子圆周运动的向心力由洛伦兹力提供,故有:
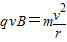 ②
②
由①②解得
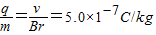
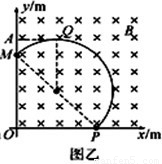
(2)设所加电场的场强大小为E,如图乙所示,当粒子经过Q点时,速度沿x轴负方向,依题意,在此时加一个沿y轴正方向的匀强电场、电场力与洛伦兹力平衡则有:
Eq=qvB
代入数据得:E=70N/C
所加电场的场强方向沿y轴正方向.
由几何关系可知,圆弧MQ所对应的圆心角为45°则射出点A对应y轴截距为:
|OA|=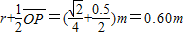
所以粒子射出磁场处A点的坐标为(0,0.60)
(3)如图丙,
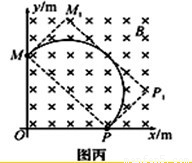 所求的最小矩形是MM1P1P
所求的最小矩形是MM1P1P
该区域面积为:s=2r2,代入r=0.35可得:
s=0.25m2
答:(1)粒子A的比荷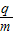 =5.0×10-7C/kg;
=5.0×10-7C/kg;
(2)如果粒子A运动过程中的某个时刻,在第一象限内再加一个匀强电场,就可以使其此后沿x轴负方向做匀速直线运动并离开第一象限,求该匀强电场的场强大小和方向,粒子射出磁场处的坐标值(0,0.6);
(3)如果要粒子A按题干要求从M处射出磁场,第一象限内的磁场可以局限在一个最小的矩形区域内,这个最小的矩形区域的面积s=0.25m2.
点评:本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.
(2)粒子做的是匀速直线运动,所以粒子处于受力平衡状态,由此可以求得电场的大小和方向.
(3)是带电粒子在有界磁场(矩形区域)中的运动,当磁场和带电粒子的轨迹相切时,磁场的面积最小
解答:解:

(1)该粒子在磁场中运动半径为r,如图甲,依题意MP连线即为该粒子在磁场中做匀速圆周运动的最小直径,由几何关系得:
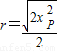 =
=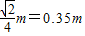 ①
①粒子圆周运动的向心力由洛伦兹力提供,故有:
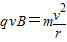 ②
②由①②解得
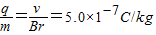

(2)设所加电场的场强大小为E,如图乙所示,当粒子经过Q点时,速度沿x轴负方向,依题意,在此时加一个沿y轴正方向的匀强电场、电场力与洛伦兹力平衡则有:
Eq=qvB
代入数据得:E=70N/C
所加电场的场强方向沿y轴正方向.
由几何关系可知,圆弧MQ所对应的圆心角为45°则射出点A对应y轴截距为:
|OA|=
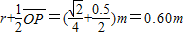
所以粒子射出磁场处A点的坐标为(0,0.60)
(3)如图丙,
 所求的最小矩形是MM1P1P
所求的最小矩形是MM1P1P该区域面积为:s=2r2,代入r=0.35可得:
s=0.25m2
答:(1)粒子A的比荷
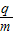 =5.0×10-7C/kg;
=5.0×10-7C/kg;(2)如果粒子A运动过程中的某个时刻,在第一象限内再加一个匀强电场,就可以使其此后沿x轴负方向做匀速直线运动并离开第一象限,求该匀强电场的场强大小和方向,粒子射出磁场处的坐标值(0,0.6);
(3)如果要粒子A按题干要求从M处射出磁场,第一象限内的磁场可以局限在一个最小的矩形区域内,这个最小的矩形区域的面积s=0.25m2.
点评:本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
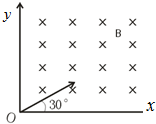
 如图所示,在第一象限存在垂直纸面向里大小为B的无限大的匀强磁场,一个质量为m,电量为q带正电的粒子从坐标原点O处以v进人磁场,粒子进入磁场时的速度方向垂直于磁场,且与x轴正方向成30.角,不计重力,则粒子在磁场中运动的时间和半径为( )
如图所示,在第一象限存在垂直纸面向里大小为B的无限大的匀强磁场,一个质量为m,电量为q带正电的粒子从坐标原点O处以v进人磁场,粒子进入磁场时的速度方向垂直于磁场,且与x轴正方向成30.角,不计重力,则粒子在磁场中运动的时间和半径为( )A、t=
| ||
B、t=
| ||
C、R=
| ||
D、R=
|
 (2011?南县模拟)如图所示,在第一象限内有垂直纸面向里的匀强磁场,一对正、负电子分别以相同速度沿与x轴成30°角从原点垂直射入磁场,则正、负电子在磁场中运动时间之比为( )
(2011?南县模拟)如图所示,在第一象限内有垂直纸面向里的匀强磁场,一对正、负电子分别以相同速度沿与x轴成30°角从原点垂直射入磁场,则正、负电子在磁场中运动时间之比为( ) 如图所示,在第一象限内有垂直纸面向里的匀强磁场,一对正、负电子分别以相同速度沿与x轴成60°角从原点射入磁场,则正、负电子在磁场中运动时间之比为( )
如图所示,在第一象限内有垂直纸面向里的匀强磁场,一对正、负电子分别以相同速度沿与x轴成60°角从原点射入磁场,则正、负电子在磁场中运动时间之比为( ) 如图所示,在第一象限内有垂直纸面向里的匀强磁场,一对质量和电荷量均相等的正、负离子(不计重力)分别以相同速度沿与x轴成30°角从原点射入磁场,则正、负离子在磁场中( )
如图所示,在第一象限内有垂直纸面向里的匀强磁场,一对质量和电荷量均相等的正、负离子(不计重力)分别以相同速度沿与x轴成30°角从原点射入磁场,则正、负离子在磁场中( )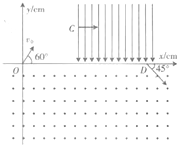 (2013?山西模拟)如图所示,在第一象限0<x<6cm的范围内,有一方向垂直于纸面向外、磁感应强度大小为B1=0.8T的圆形匀强磁场区域(图中未画出),在x>6cm的范围内有沿y轴负方向的匀强电场;第三、四象限内有垂直纸面向外的匀强磁场,磁感应强度B2的大小未知.一个质量m=8.0×10-l2kg、电荷量q=2.0×l0-6C的带正电的粒子,以v0=4.0×l03m/s的速度从坐标原点O沿与x轴正方向成60°角射出,经圆形匀强磁场区域后平行x轴方向到达C(6cm,4cm )点,之后从C点垂直电场方向射入匀强电场中,并从D点沿与x轴正方向成45°角进入匀强磁场B2中,最后恰好能返回到O点.不计带电粒子的重力,求:
(2013?山西模拟)如图所示,在第一象限0<x<6cm的范围内,有一方向垂直于纸面向外、磁感应强度大小为B1=0.8T的圆形匀强磁场区域(图中未画出),在x>6cm的范围内有沿y轴负方向的匀强电场;第三、四象限内有垂直纸面向外的匀强磁场,磁感应强度B2的大小未知.一个质量m=8.0×10-l2kg、电荷量q=2.0×l0-6C的带正电的粒子,以v0=4.0×l03m/s的速度从坐标原点O沿与x轴正方向成60°角射出,经圆形匀强磁场区域后平行x轴方向到达C(6cm,4cm )点,之后从C点垂直电场方向射入匀强电场中,并从D点沿与x轴正方向成45°角进入匀强磁场B2中,最后恰好能返回到O点.不计带电粒子的重力,求: