题目内容
如图所示，某货物仓库，需将生产成品用传送带从底端传递到高度为H的高处存放，货物从静止开始轻放到传送带的最下端，已知货物与传送带间的动摩擦因数为μ＝，传送带始终保持恒定速度运动。若想用最短时间将货物匀加速的运送至顶端，则传送带与水平面夹角θ应设计为多大？最短时间为多少?（传送带长度可随设计需要而变化，g＝10m/s2）
当θ＝30°时，货物运动最短时间为t＝2
解析:
：对物体受力分析，受到重力G、弹力N和摩擦力f，物体向上运动的加速度为：
a＝μgcosθ－gsinθ （3分）
物体做匀加速运动则：
＝(μgcosθ－gsinθ)t2 （3分）
物体上升运动的时间：t＝ （4分）
而sinθ(μcosθ－sinθ)＝μsin2θ－＝ (μsin2θ＋cos2θ－1)
又μsin2θ＋cos2θ＝sin(2θ＋φ)
因sinφ＝，所以φ＝30°
故当θ＝30°时，μsin2θ＋cos2θ取最大值为2 （3分）
所以，当θ＝30°时，货物运动最短时间为t＝2 （3分）
练习册系列答案
相关题目
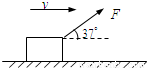
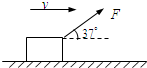如图所示，商场工作人员用与水平方向成37°斜向上、大小为200N的力F拉着货物沿水平地面做匀速运动，货物的质量为52kg，速度大小为8m/s，某时刻撤去拉力后，货物滑行了一段距离停下（cos37°=0.8，sin37°=0.6）．求：
如图所示，某货物仓库，需将生产成品用传送带从底端传递到高度为H的高处存放，货物从静止开始轻放到传送带的最下端，已知货物与传送带间的动摩擦因数为μ=
，传送带始终保持恒定速度运动。若想用最短时间将货物匀加速的运送至顶端，则传送带与水平面夹角θ应设计为多大？最短时间为多少?（传送带长度可随设计需要而变化，g＝10m/s2）
