题目内容
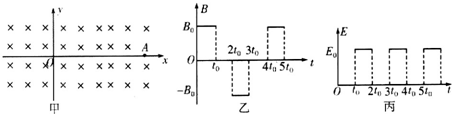
9. 如图所示,一根光滑绝缘细杆与水平面成α=30°的角倾斜固定.细杆的一部分处在场强方向水平向右的匀强电场中,场强E=2×104N/C.在细杆上套有一个带电量为q=-1.73×10-5C、质量为m=3×10-2kg的小球.现使小球从细杆的顶端A由静止开始沿杆滑下,并从B点进入电场,小球在电场中滑至最远处的C点.已知AB间距离x1=0.4m,g=10m/s2.求:
如图所示,一根光滑绝缘细杆与水平面成α=30°的角倾斜固定.细杆的一部分处在场强方向水平向右的匀强电场中,场强E=2×104N/C.在细杆上套有一个带电量为q=-1.73×10-5C、质量为m=3×10-2kg的小球.现使小球从细杆的顶端A由静止开始沿杆滑下,并从B点进入电场,小球在电场中滑至最远处的C点.已知AB间距离x1=0.4m,g=10m/s2.求:(1)小球在B点的速度vB;
(2)小球进入电场后滑行的最大距离x2.
分析 (1)小球在AB段运动的过程中,机械能守恒,结合机械能守恒定律求出小球在B点的速度大小.
(2)根据牛顿第二定律求出小球进入电场后的加速度大小,结合速度位移公式求出小球进入电场后滑行的最大距离.
解答 解:(1)小球在AB段滑动过程中,由机械能守恒
mgx1sinα=$\frac{1}{2}$$m{{v}_{B}}^{2}$
代入数据解得vB=2 m/s.
(2)小球进入匀强电场后,在电场力和重力的作用下,由牛顿第二定律可得加速度
a2=$\frac{mgsinα-qEcosα}{m}$=$\frac{0.3×\frac{1}{2}-1.73×1{0}^{-5}×2×1{0}^{4}×\frac{\sqrt{3}}{2}}{0.03}m/{s}^{2}$=-5 m/s2
小球进入电场后还能滑行到最远处C点,BC的距离为
x2=$\frac{-{{v}_{B}}^{2}}{2{a}_{2}}=\frac{-4}{-10}m$=0.4 m.
答:
(1)小球在B点的速度为2m/s;
(2)小球进入电场后滑行的最大距离为0.4m.
点评 解决本题的关键知道小球在整个过程中的运动规律,结合牛顿第二定律和运动学公式综合求解,对于第一问,也可以根据动力学知识求解.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
17.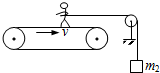 如图所示为一种测定运动员体能的装置,运动员的质量为m1,绳的一端拴在腰间并沿水平方向跨过滑轮(不计滑轮质量及摩擦),绳的下端悬挂一个质量为m2的重物,人用力蹬传送带而人的重心不动,使传送带以速率v匀速向右运动.下面说法中正确的是( )
如图所示为一种测定运动员体能的装置,运动员的质量为m1,绳的一端拴在腰间并沿水平方向跨过滑轮(不计滑轮质量及摩擦),绳的下端悬挂一个质量为m2的重物,人用力蹬传送带而人的重心不动,使传送带以速率v匀速向右运动.下面说法中正确的是( )
 如图所示为一种测定运动员体能的装置,运动员的质量为m1,绳的一端拴在腰间并沿水平方向跨过滑轮(不计滑轮质量及摩擦),绳的下端悬挂一个质量为m2的重物,人用力蹬传送带而人的重心不动,使传送带以速率v匀速向右运动.下面说法中正确的是( )
如图所示为一种测定运动员体能的装置,运动员的质量为m1,绳的一端拴在腰间并沿水平方向跨过滑轮(不计滑轮质量及摩擦),绳的下端悬挂一个质量为m2的重物,人用力蹬传送带而人的重心不动,使传送带以速率v匀速向右运动.下面说法中正确的是( )| A. | 绳子拉力对人做正功 | |
| B. | 人对传送带做正功 | |
| C. | 运动时间t后,运动员的体能消耗约为m1gvt | |
| D. | 运动时间t后,运动员的体能消耗约为(m1+m2)gvt |
14.核能安全是核电站面临的严峻的问题.核泄漏中的钚(Pu)是一种具有放射性的超铀元素,一旦侵入人体,就会潜伏在人体肺部、骨骼等组织细胞中,破坏细胞基因,提高罹患癌症的风险.已知钚的一种同位素${\;}_{94}^{239}$Pu的半衰期为24100年,其衰变方程为${\;}_{94}^{239}$Pu→X+${\;}_{2}^{4}$He+γ,下列有关说法正确的是( )
| A. | X原子核中含有143个中子 | |
| B. | 100个${\;}_{94}^{239}$Pu经过24100年后一定还剩余50个 | |
| C. | 由于衰变时释放巨大能量,根据E=mc2,衰变过程中总质量增加 | |
| D. | 衰变发出的γ放射线是波长很短的光子,具有很强的穿透能力 |
19.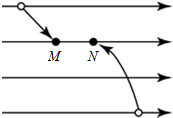 如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,不计重力,则( )
如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,不计重力,则( )
 如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,不计重力,则( )
如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,不计重力,则( )| A. | M的带电量比N的大 | B. | M带负电荷,N带正电荷 | ||
| C. | 静止时M受到的合力比N的大 | D. | 移动过程中匀强电场对M做负功 |
 如图所示,一倾角为30°的光滑斜面固定在地面上,一质量为m的小木块在水平力F的作用下静止在斜面上,若只改变F的方向不改变F的大小,仍使木块静止,则此时力F与水平面的夹角为60°.
如图所示,一倾角为30°的光滑斜面固定在地面上,一质量为m的小木块在水平力F的作用下静止在斜面上,若只改变F的方向不改变F的大小,仍使木块静止,则此时力F与水平面的夹角为60°.
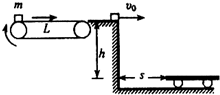 如图所示,水平传送带的速度为4.0m/s,它的右端与等高的光滑水平平台相接触.将一质量为m=1kg的工件(可看成质点)轻轻放在传送带的左端,工件与传送带间的动摩擦因数μ=0.3,经过一段时间工件从光滑水平平台上滑出,恰好落在静止在平台下的小车的左端,小车的质量为M=2kg,小车与地面的摩擦可忽略.已知平台与小车的高度差h=0.8m,小车左端距平台右端的水平距离为s=1.2m,取g=10m/s2,求:
如图所示,水平传送带的速度为4.0m/s,它的右端与等高的光滑水平平台相接触.将一质量为m=1kg的工件(可看成质点)轻轻放在传送带的左端,工件与传送带间的动摩擦因数μ=0.3,经过一段时间工件从光滑水平平台上滑出,恰好落在静止在平台下的小车的左端,小车的质量为M=2kg,小车与地面的摩擦可忽略.已知平台与小车的高度差h=0.8m,小车左端距平台右端的水平距离为s=1.2m,取g=10m/s2,求: