题目内容
17. 一定质量的理想气体被活塞封闭在竖直放置的绝热气缸内,活塞的质量为1kg,横截面积s=5cm2,活塞可沿气缸壁无摩擦滑动且不漏气.开始活塞距气缸底部10cm,气体温度为27℃,现在对气缸内气体缓缓加热,活塞上升了5cm,已知大气压强p0=1.0×105Pa,g=10m/s2,求:
一定质量的理想气体被活塞封闭在竖直放置的绝热气缸内,活塞的质量为1kg,横截面积s=5cm2,活塞可沿气缸壁无摩擦滑动且不漏气.开始活塞距气缸底部10cm,气体温度为27℃,现在对气缸内气体缓缓加热,活塞上升了5cm,已知大气压强p0=1.0×105Pa,g=10m/s2,求:(Ⅰ)最后气缸内气体的温度;
(Ⅱ)保持气缸内气体满足(Ⅰ)问中的温度,使整个装置竖直向上做匀加速运动,达到稳定状态时活塞又回到原来的位置,则整个装置的加速度为多少?
分析 (Ⅰ)温度升高过程,封闭气体做等压变化,根据盖吕萨克定律列式求解;
(Ⅱ)等温变化,根据玻意而定律列式求解.
解答 解:(Ⅰ)温度升高过程,封闭气体做等压变化,根据盖吕萨克定律得:
$\frac{{L}_{1}S}{{T}_{1}}=\frac{{(L}_{1}+△L)S}{{T}_{2}}$
代入数据解得:${T}_{2}=\frac{{L}_{1}+△L}{{L}_{1}}{T}_{1}=\frac{10+5}{10}×(273+27)K=450K$
即:t2=450-273℃=177℃
(Ⅱ)封闭气体做等温变化,
有玻意而定律得:P1(L1+△L)S=P2L1S ①
对活塞根据平衡得:初态压强为:${P}_{1}={P}_{0}+\frac{mg}{S}=1.0×1{0}^{5}+\frac{1×10}{5×1{0}^{-4}}Pa=1.2×1{0}^{5}Pa$ ②
末态根据牛顿第二定律得:P2S-mg-P0S=ma ③
①②③联立解得:a=30m/s2
答:(Ⅰ)最后气缸内气体的温度为177℃;
(Ⅱ)整个装置的加速度为30m/s2
点评 本题考察气体实验定律和力学综合题,关键是以活塞为研究对象,根据平衡和牛顿第二定律列式求解压强.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
7. 如图所示,水平传送带以速度v1匀速运动,小物体P、Q由通过光滑定滑轮的不可伸长的轻绳相连,t=0时刻P在传送带左端具有速度v2,己知v1>v2,P与定滑轮间的绳水平.不计定滑轮质量,绳足够长,物体与传送带之间的最大静摩擦力和滑动摩擦力相等.从最初直到物体P从传送带离开的过程,以下判断正确的是( )
如图所示,水平传送带以速度v1匀速运动,小物体P、Q由通过光滑定滑轮的不可伸长的轻绳相连,t=0时刻P在传送带左端具有速度v2,己知v1>v2,P与定滑轮间的绳水平.不计定滑轮质量,绳足够长,物体与传送带之间的最大静摩擦力和滑动摩擦力相等.从最初直到物体P从传送带离开的过程,以下判断正确的是( )
 如图所示,水平传送带以速度v1匀速运动,小物体P、Q由通过光滑定滑轮的不可伸长的轻绳相连,t=0时刻P在传送带左端具有速度v2,己知v1>v2,P与定滑轮间的绳水平.不计定滑轮质量,绳足够长,物体与传送带之间的最大静摩擦力和滑动摩擦力相等.从最初直到物体P从传送带离开的过程,以下判断正确的是( )
如图所示,水平传送带以速度v1匀速运动,小物体P、Q由通过光滑定滑轮的不可伸长的轻绳相连,t=0时刻P在传送带左端具有速度v2,己知v1>v2,P与定滑轮间的绳水平.不计定滑轮质量,绳足够长,物体与传送带之间的最大静摩擦力和滑动摩擦力相等.从最初直到物体P从传送带离开的过程,以下判断正确的是( )| A. | 物体P可能先减速后加速 | B. | 物体P可能先加速后减速 | ||
| C. | 物体P可能先加速后匀速 | D. | 物体P可能先减速后匀速 |
8.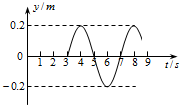 一列简谐横波沿直线传播.以波源O由平衡位置开始振动为计时起点,质点A的振动图象如图所示,已知O、A的平衡位置相距0.9m.以下判断正确的是( )
一列简谐横波沿直线传播.以波源O由平衡位置开始振动为计时起点,质点A的振动图象如图所示,已知O、A的平衡位置相距0.9m.以下判断正确的是( )
 一列简谐横波沿直线传播.以波源O由平衡位置开始振动为计时起点,质点A的振动图象如图所示,已知O、A的平衡位置相距0.9m.以下判断正确的是( )
一列简谐横波沿直线传播.以波源O由平衡位置开始振动为计时起点,质点A的振动图象如图所示,已知O、A的平衡位置相距0.9m.以下判断正确的是( )| A. | 波源起振方向沿y轴正方向 | B. | 波速大小为0.4m/s | ||
| C. | 波长为1.2m | D. | t=3s时,波源O的动能最大 |
5.下列说法中正确的是( )
| A. | 根据狭义相对论物体运动质量和静止质量的关系m=$\frac{{m}_{0}}{\sqrt{1-\frac{{v}^{2}}{{c}^{2}}}}$,可以得出物体的速度可能达到光速 | |
| B. | 考虑到各种综合因素,远距离输电,输电电压越高越好 | |
| C. | 野外高压输电线在三条输电线的上方还有两条导线,它们与大地相连,形成一个稀疏的金属“网”,把高压线屏蔽起来,免遭雷击 | |
| D. | 电容器外壳上标的是额定电压,也是该电容的击穿电压 |
12.18世纪,数学家莫佩尔蒂和哲学家伏尔泰,曾设想“穿透”地球:假设能够沿着地球两极连线开凿一条沿着地轴的隧道贯穿地球,一个人可以从北极入口由静止自由落入隧道中,忽略一切阻力,此人可以从南极出口飞出,则以下说法正确的是(已知此人的质量m=50kg;地球表面处重力加速度取g=10m/s2;地球半径R=6.4×106m;假设地球可视为质量分布均匀的球体.均匀球壳对壳内任一点的质点合引力为零)( )
| A. | 人与地球构成的系统,由于重力发生变化,故机械能不守恒 | |
| B. | 人在下落过程中,受到的万有引力与到地心的距离成二次方反比 | |
| C. | 人从北极开始下落,直到经过地心的过程中,万有引力对人做功W=1.6×109J | |
| D. | 当人下落经过距地心$\frac{R}{2}$瞬间,人的瞬时速度大小为4×103m/s |
6. 如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )
如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )
 如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )
如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )| A. | 168cm | B. | 56cm | C. | 42cm | D. | 30cm | ||||
| E. | 24cm |
7.“静止”在赤道上空的地球同步气象卫星把广阔视野内的气象数据发回地面,为天气预报提供准确、全面和及时的气象资料.设地球同步气象卫星的轨道半径是地球半径的n倍,则该地球同步气象卫星的( )
| A. | 向心加速度是地球表面重力加速度的$\frac{1}{n}$倍 | |
| B. | 向心加速度是地球表面重力加速度的$\sqrt{\frac{1}{n}}$倍 | |
| C. | 运行速度是近地卫星运行速度的$\frac{1}{n}$倍 | |
| D. | 运行速度是近地卫星运行速度的$\sqrt{\frac{1}{n}}$倍 |
 如图所示,封闭有一定质量理想气体的气缸固定在水平桌面上,开口向右放置,活塞的横截面积为S.活塞通过不可伸长的轻绳连接了一个质量为m=$\frac{{ρ}_{0}S}{2g}$的小物体,轻绳跨在定滑轮上.开始时汽缸内外压强相同,均为大气压p0(为已知).汽缸内气体的温度为T0,轻绳恰好处在伸直状态.不计摩擦,重力加速度为g,现缓慢降低汽缸内温度,求:
如图所示,封闭有一定质量理想气体的气缸固定在水平桌面上,开口向右放置,活塞的横截面积为S.活塞通过不可伸长的轻绳连接了一个质量为m=$\frac{{ρ}_{0}S}{2g}$的小物体,轻绳跨在定滑轮上.开始时汽缸内外压强相同,均为大气压p0(为已知).汽缸内气体的温度为T0,轻绳恰好处在伸直状态.不计摩擦,重力加速度为g,现缓慢降低汽缸内温度,求: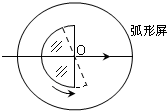 用如图的装置测定玻璃的折射率,半圆形玻璃砖与弧形屏固定,半圆形玻璃砖按图中实线位置放置,使一激光束从玻璃弧面左侧入射并垂直直径平面通过圆心射出玻璃砖,记下入射光束在圆弧形屏上所对应位置的刻度,使玻璃砖以圆心O为轴逆时针缓慢转动,同时观察直径平面一侧出射光线的变化;出射光线不断向下偏转并越来越暗,直到刚好看不到出射光线为止,并记下这时入射光线在弧形屏位置的刻度.这个过程半圆形玻璃砖转过的角度θ就是光束从玻璃射入空气的临界角,玻璃折射率的表达式n=$\frac{1}{sinθ}$.
用如图的装置测定玻璃的折射率,半圆形玻璃砖与弧形屏固定,半圆形玻璃砖按图中实线位置放置,使一激光束从玻璃弧面左侧入射并垂直直径平面通过圆心射出玻璃砖,记下入射光束在圆弧形屏上所对应位置的刻度,使玻璃砖以圆心O为轴逆时针缓慢转动,同时观察直径平面一侧出射光线的变化;出射光线不断向下偏转并越来越暗,直到刚好看不到出射光线为止,并记下这时入射光线在弧形屏位置的刻度.这个过程半圆形玻璃砖转过的角度θ就是光束从玻璃射入空气的临界角,玻璃折射率的表达式n=$\frac{1}{sinθ}$.