题目内容
 回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示.设D形盒半径为R.若用回旋加速器加速质子时,匀强磁场的磁感应强度为B,高频交流电频率为f.则下列说法正确的是( )
回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示.设D形盒半径为R.若用回旋加速器加速质子时,匀强磁场的磁感应强度为B,高频交流电频率为f.则下列说法正确的是( )分析:粒子在磁场中运动时,洛伦兹力提供向心力,满足qvB=m
运动周期T=
=
(电场中加速时间忽略不计).对公式进行简单推导后,便可解此题.
| v2 |
| r |
| 2πr |
| v |
| 2πm |
| qB |
解答:解:A、考虑到狭义相对论,任何物体速度不可能超过光速,故A错误;
B、T=
得:v=2πrf当r=R时,v最大,此v=2πfR,不会超过此值,故B错误;
C、qvB=m
得:v=
当r=R时,v最大,v=
由此可知质子的最大速度只与粒子本身的荷质比,加速器半径,和磁场大小有关,故C正确;
D、此加速器加速电场周期T=
加速α粒子时T=
两个周期不同,不能加速α粒子.故D错误;
故选:C.
B、T=
| 2πr |
| v |
C、qvB=m
| v2 |
| r |
| qBr |
| m |
| qBR |
| m |
D、此加速器加速电场周期T=
| 2πm |
| qB |
| 4πm |
| qB |
故选:C.
点评:理解回旋加速器工作原理,熟练运用相关公式,便可解出此题.

练习册系列答案
相关题目
 回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电两极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的匀强电场,使粒子在通过狭缝时都能得到加速.两D形金属盒处于垂直于盒底面的匀强磁场中,如图所示,设匀强磁场的磁感应强度为B,D形金属盒的半径为R,狭缝间的距离为d,匀强电场间的加速电压为U,要增大带电粒子(电荷量为q质量为m,不计重力)射出时的动能,则下列方法中正确的是( )
回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电两极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的匀强电场,使粒子在通过狭缝时都能得到加速.两D形金属盒处于垂直于盒底面的匀强磁场中,如图所示,设匀强磁场的磁感应强度为B,D形金属盒的半径为R,狭缝间的距离为d,匀强电场间的加速电压为U,要增大带电粒子(电荷量为q质量为m,不计重力)射出时的动能,则下列方法中正确的是( )| A、增大匀强电场间的加速电压 | B、减小狭缝间的距离 | C、增大磁场的磁感应强度 | D、增大D形金属盒的半径 |
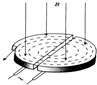 回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示.设D形盒半径为R.若用回旋加速器加速质子(氢核)时,匀强磁场的磁感应强度为B,高频交流电频率为f.质子质量为m,电荷量为e.则下列说法正确的是( )
回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示.设D形盒半径为R.若用回旋加速器加速质子(氢核)时,匀强磁场的磁感应强度为B,高频交流电频率为f.质子质量为m,电荷量为e.则下列说法正确的是( )| A、质子被加速后的最大速度不可能超过2πRf | ||
B、质子被加速后的最大动能Ek不可能超过
| ||
| C、质子被加速后的最大动能与狭缝间的加速电压、加速次数无关 | ||
| D、改变B和f,该回旋加速器也能用于加速α粒子(即氦核) |
 (2008?武昌区模拟)回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,要增大带电粒子射出时的动能,则下列说法中正确的是( )
(2008?武昌区模拟)回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,要增大带电粒子射出时的动能,则下列说法中正确的是( ) 回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,则下列说法正确的是( )
回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,则下列说法正确的是( ) (2012?丹东模拟)回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示.设D形盒半径为R.若用回旋加速器加速质子时,匀强磁场的磁感应强度为B,高频交流电频率为f.则下列说法正确的是( )
(2012?丹东模拟)回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示.设D形盒半径为R.若用回旋加速器加速质子时,匀强磁场的磁感应强度为B,高频交流电频率为f.则下列说法正确的是( )