题目内容
2.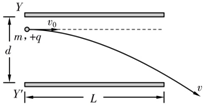 如图所示,Y和Y′是真空中一对水平放置的平行金属板,板间距离为d,板长为L,两板间电势差为U,板间电场可视为匀强电场.现有一电荷量为+q、质量为m的带电粒子,以水平初速度v0射入板间.已知该粒子能射出金属板,求:
如图所示,Y和Y′是真空中一对水平放置的平行金属板,板间距离为d,板长为L,两板间电势差为U,板间电场可视为匀强电场.现有一电荷量为+q、质量为m的带电粒子,以水平初速度v0射入板间.已知该粒子能射出金属板,求:(1)若不计粒子重力,带电粒子射出金属板时速度v的大小;
(2)若不计粒子重力,在带电粒子通过平行金属板的过程中,电场力所做的功W.
(3)极板间既有电场也有重力场.电势反映了静电场各点的能的性质,请写出电势φ的定义式.类比电势的定义方法,在重力场中建立“重力势”的φG概念.
分析 (1)粒子做类平抛运动,水平方向匀速,竖直方向匀加速,故可求得速度;
(2)利用动能定理求的电场力做功;
(3)电势是电荷在某点的电势能与电荷量的比值,由此分析重力势的定义式.
解答 解:(1)金属板间匀强电场的场强E=$\frac{U}{d}$,
在平行于金属板的方向,带电粒子以速度v0做匀速直线运动的时间:t=$\frac{L}{{v}_{0}}$,
在垂直于金属板的方向,带电粒子做初速度为零的匀加速运动.
根据牛顿第二定律,粒子的加速度a=$\frac{qE}{m}$,
所以粒子射出金属板时,在垂直金属板方向的分速度${v}_{⊥}=at=\frac{qUL}{md{v}_{0}}$,
所以带电粒子射出金属板时速度v=$\sqrt{{v}_{0}^{2}+{v}_{⊥}^{2}}$=$\sqrt{{v}_{0}^{2}+\frac{{U}^{2}{q}^{2}{L}^{2}}{{m}^{2}{d}^{2}{v}_{0}^{2}}}$;
(2)根据动能理可求得,在此过程中电场力所做的功为:
W=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{0}^{2}$=$\frac{{U}^{2}{q}^{2}{L}^{2}}{2m{d}^{2}{v}_{0}^{2}}$;
(3)电场中,电势的定义为电势能与电荷量的比值,即:$φ=\frac{{E}_{P}}{q}$,
根据电势的定义可以这样定义重力势:物体在某点的重力势能与质量的比值,即:${φ}_{G}=\frac{{E}_{P}}{m}$.
答:(1)带电粒子射出金属板时速度v的大小$\sqrt{{v}_{0}^{2}+\frac{{U}^{2}{q}^{2}{L}^{2}}{{m}^{2}{d}^{2}{v}_{0}^{2}}}$;
(2)在带电粒子通过平行金属板的过程中,电场力所做的功为$\frac{{U}^{2}{q}^{2}{L}^{2}}{2m{d}^{2}{v}_{0}^{2}}$;
(3)电势φ的定义式为$φ=\frac{E_P}{q}$,在重力场中建立“重力势”${φ_G}=\frac{E_P}{m}$.
点评 带电粒子在电场中的运动,若垂直电场线进入则做类平抛运动,要将运动分解为沿电场线和垂直于电场线两个方向进行分析,利用直线运动的规律进行求解.

 如图所示,两个质量相等的带电粒子a、b在同一位置A以大小相同的速度射入同一匀强磁场,两粒子的入射方向与磁场边界的夹角分别为30°和60°,经磁场偏转后两粒子都经过B点,AB连线与磁场边界垂直,则( )
如图所示,两个质量相等的带电粒子a、b在同一位置A以大小相同的速度射入同一匀强磁场,两粒子的入射方向与磁场边界的夹角分别为30°和60°,经磁场偏转后两粒子都经过B点,AB连线与磁场边界垂直,则( )| A. | a粒子带正电,b粒子带负电 | B. | 两粒子的轨道半径之比Ra:Rb=$\sqrt{3}$:1 | ||
| C. | 两粒子所带电荷量之比qa:qb=$\sqrt{3}$:1 | D. | 两粒子的运动时间之比ta:tb=2:$\sqrt{3}$ |
 如图所示,A板发出的电子经加速后,水平射入水平放置的两平行金属板间,金属板间所加的电压为U,电子最终打在荧光屏P上,关于电子的运动,下列说法中正确的是( )
如图所示,A板发出的电子经加速后,水平射入水平放置的两平行金属板间,金属板间所加的电压为U,电子最终打在荧光屏P上,关于电子的运动,下列说法中正确的是( )| A. | 滑动触头向右移动时,电子打在荧光屏上的位置上升 | |
| B. | 滑动触头向左移动时,电子打在荧光屏上的位置上升 | |
| C. | 电压U增大时,电子打在荧光屏上的速度大小不变 | |
| D. | 电压U增大时,电子从发出到打在荧光屏上的时间不变 |

| A. | 3$\sqrt{2}$V | B. | 0.02s | C. | 0.01s | D. | 3V |
 月球探测器在月面实现软着陆是非常困难的,探测器接触地面瞬间速度为竖直向下的v1,大于要求的软着陆速度v0,为此,科学家们设计了一种叫电磁阻尼缓冲装置,其原理如图所示.主要部件为缓冲滑块K和绝缘光滑的缓冲轨道MN、PQ.探测器主体中还有超导线圈(图中未画出),能在两轨道间产生垂直于导轨平面的匀强磁场.导轨内的缓冲滑块由高强绝缘材料制成,滑块K上绕有闭合单匝矩形线圈abcd,线圈的总电阻为R,ab边长为L.当探测器接触地面时,滑块K立即停止运动,此后线圈与轨道间的磁场发生作用,使探测器主体做减速运动,从而实现缓冲.已知装置中除缓冲滑块(含线圈)外的质量为m,月球表面的重力加速度为$\frac{g}{6}$,不考虑运动磁场产生的电场.
月球探测器在月面实现软着陆是非常困难的,探测器接触地面瞬间速度为竖直向下的v1,大于要求的软着陆速度v0,为此,科学家们设计了一种叫电磁阻尼缓冲装置,其原理如图所示.主要部件为缓冲滑块K和绝缘光滑的缓冲轨道MN、PQ.探测器主体中还有超导线圈(图中未画出),能在两轨道间产生垂直于导轨平面的匀强磁场.导轨内的缓冲滑块由高强绝缘材料制成,滑块K上绕有闭合单匝矩形线圈abcd,线圈的总电阻为R,ab边长为L.当探测器接触地面时,滑块K立即停止运动,此后线圈与轨道间的磁场发生作用,使探测器主体做减速运动,从而实现缓冲.已知装置中除缓冲滑块(含线圈)外的质量为m,月球表面的重力加速度为$\frac{g}{6}$,不考虑运动磁场产生的电场.



 如图所示,空间存在着范围足够大、水平向左的匀强电场,在竖直虚线PM的左侧有垂直纸面向里的匀强磁场,磁感应强度大小为B=$\frac{m}{q}\sqrt{\frac{g}{2R}}$.一绝缘U形弯杆由两段直杆和一半径为R的半圆环组成,固定在纸面所在的竖直平面内.PQ、MN水平且足够长,半圆环在磁场边界左侧,P、M点在磁场边界线上,A点为圆弧上的一点,NMAP段是光滑的.现有一质量为m、带电荷量为+q的小环套在半圆环上,恰好在A点保持静止,半径OA与虚线所成夹角为θ=37°.现将带电小环由P点无初速度释放(sin37°=0.6,cos37°=0.8).求:
如图所示,空间存在着范围足够大、水平向左的匀强电场,在竖直虚线PM的左侧有垂直纸面向里的匀强磁场,磁感应强度大小为B=$\frac{m}{q}\sqrt{\frac{g}{2R}}$.一绝缘U形弯杆由两段直杆和一半径为R的半圆环组成,固定在纸面所在的竖直平面内.PQ、MN水平且足够长,半圆环在磁场边界左侧,P、M点在磁场边界线上,A点为圆弧上的一点,NMAP段是光滑的.现有一质量为m、带电荷量为+q的小环套在半圆环上,恰好在A点保持静止,半径OA与虚线所成夹角为θ=37°.现将带电小环由P点无初速度释放(sin37°=0.6,cos37°=0.8).求: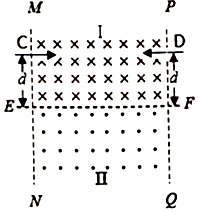 正负电子对撞机是使正负电子以相同速率对撞(撞前速度在同一直线上的碰撞)并进行高能物理研究的实验装置,该装置一般由高能加速器(同步加速器或直线加速器)、环形储存室(把高能加速器在不同时间加速出来的电子束进行积累的环形真空室)和对撞测量区(对撞时发生的新粒子、新现象进行测量)三个部分组成.为了使正负电子在测量区内不同位置进行对撞,在对撞测量区内设置两个方向相反的匀强磁场区域.对撞区域设计的简化原理如图所示:MN和PQ为足够长的竖直边界,水平边界EF将整个区域分成上下两部分,Ⅰ区域的磁场方向垂直纸面向内,Ⅱ区域的磁场方向垂直纸面向外,磁感应强度大小均为B.现有一对正负电子以相同速率分别从注入口C和注入口D同时水平射入,在对撞测量区发生对撞.已知两注入口到EF的距离均为d,边界MN和PQ的间距为L,正电子的质量为m,电量为+e,负电子的质量为m,电量为-e.
正负电子对撞机是使正负电子以相同速率对撞(撞前速度在同一直线上的碰撞)并进行高能物理研究的实验装置,该装置一般由高能加速器(同步加速器或直线加速器)、环形储存室(把高能加速器在不同时间加速出来的电子束进行积累的环形真空室)和对撞测量区(对撞时发生的新粒子、新现象进行测量)三个部分组成.为了使正负电子在测量区内不同位置进行对撞,在对撞测量区内设置两个方向相反的匀强磁场区域.对撞区域设计的简化原理如图所示:MN和PQ为足够长的竖直边界,水平边界EF将整个区域分成上下两部分,Ⅰ区域的磁场方向垂直纸面向内,Ⅱ区域的磁场方向垂直纸面向外,磁感应强度大小均为B.现有一对正负电子以相同速率分别从注入口C和注入口D同时水平射入,在对撞测量区发生对撞.已知两注入口到EF的距离均为d,边界MN和PQ的间距为L,正电子的质量为m,电量为+e,负电子的质量为m,电量为-e.