��Ŀ����
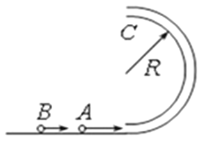
����Ŀ��Ħ�������Ǵ���װ���е�һ����Ҫģ�ͣ���ͼ��ʾ������ˮƽ���õ����̿�Ħ��������������O��O'�ֱ�Ϊ�����̵����ģ���֪�������̵İ뾶��r����r��=3��1���ڹ���ʱ�����̲��������������Ϸֱ��������ͬ�ֲ����Ƴɵ���ȫ��ͬ��С����A��B�������������̼�Ķ�Ħ��������ͬ���ӻ���Ħ�����������Ħ���������������������O��O'�ļ��RA=2RB�����������ɾ�ֹ��ʼ������ת����������ת�������ӣ�������������ȷ���У� ��

A.С����A��B����������Ծ�ֹʱ�����ٶ�֮��Ϊ����������=1��3
B.С����A��B����������Ծ�ֹʱ�����ļ��ٶ�֮��ΪaA��aB=2��9
C.ת�����Ӻ�С����A�ȷ�������
D.ת�����Ӻ�С����B�ȷ�������
���𰸡�ABD
��������
A�����������ҵİ뾶Ϊr���������֪�����̱�Ե�����ٶ�v��С��ȣ��ɣ�
v����r
r����r����3��1
�ɵã�
������������1��3
���Ի���������̻���ǰ��A��B�Ľ��ٶ�֮��Ϊ1��3����A��ȷ��
B����������̿�ʼ����ǰ�����ݣ�
![]()
RA��RB��2��1
������������1��3
��A��B�����ļ��ٶ�֮��Ϊ��
aA��aB��2��9
��B��ȷ��
CD��������ɵ��������Ħ�����ֱ�Ϊ��
![]()
![]()
���Ħ����֮�ȣ�
![]()
ת�������ܵľ�Ħ����֮��Ϊ��
![]()
���Ϸ����ɵû���B�ȴﵽ���Ħ�������ȿ�ʼ��������C����D��ȷ��