题目内容
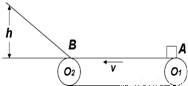
如图所示,皮带在轮O1、O2带动下以速度v匀速转动,皮带与轮之间不打滑.皮带AB段 长为L,皮带轮左端B处有一光滑小圆弧与一光滑斜面相连接.物体无初速度放上皮带右端后,能在皮带带动下向左运动,并滑上斜面.已知物体与皮带间的动摩擦因数为μ,且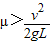 .求:
.求:(1)若物体无初速度放上皮带的右端A处,则其运动到左端B处所需的时间;
(2)若物体无初速度放上皮带的右端A处,则其运动到左端B处过程中所产生的热量;
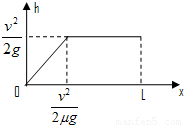
(3)物体无初速度放上皮带的不同位置,则其沿斜面上升的最大高度也不同.设物体放上皮带时离左端B的距离为x,物体沿斜面上升的最大高度为h,请画出h-x图象.
【答案】分析:(1)物块滑上传送带先做匀加速直线运动,当达到传送带速度时,一起做匀速直线运动,求出匀加速直线运动和匀速直线运动的时间之和,即为物体从右端滑到左端的时间.
(2)求解出滑块与皮带间的相对位移,然后Q=f?△S求解热量;
(3)分一直加速和先加速后匀速两种情况讨论,根据动能定理求解出最大高度后龄列式求解.
解答:解:(1)由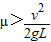 可得
可得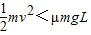 ,即物体到达B之前就与传送带共速;
,即物体到达B之前就与传送带共速;
设物体加速度为a,则 μmg=ma ①
加速阶段的时间为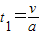 ②
②
加速阶段的位移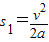 ③
③
匀速阶段的时间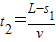 ④
④
总时间 t=t1+t2 ⑤
由①②③④⑤解得:

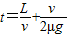
(2)物体在加速阶段与传送带的相对位移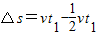 ⑥
⑥
发热量Q=μmg△s ⑦
由①②⑥⑦解得
(3)当x≤S1时,物体一直加速,到B的速度为v1,则v12=2μgx
又 mv12=mgh
mv12=mgh
∴h=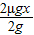 =μx
=μx
当x>S1时,物体先加速后匀速,到达B时速度均为v
 mv2=mgh
mv2=mgh
h′=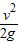
如图所示
答:(1)若物体无初速度放上皮带的右端A处,则其运动到左端B处所需的时间为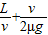 ;
;
(2)若物体无初速度放上皮带的右端A处,则其运动到左端B处过程中所产生的热量为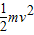 ;
;
(3)如图所示.
点评:解决本题的关键根据物块的受力,判断物体的运动状况,加速度是联系前后的桥梁.
(2)求解出滑块与皮带间的相对位移,然后Q=f?△S求解热量;
(3)分一直加速和先加速后匀速两种情况讨论,根据动能定理求解出最大高度后龄列式求解.
解答:解:(1)由
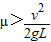 可得
可得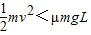 ,即物体到达B之前就与传送带共速;
,即物体到达B之前就与传送带共速;设物体加速度为a,则 μmg=ma ①
加速阶段的时间为
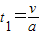 ②
②加速阶段的位移
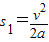 ③
③匀速阶段的时间
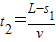 ④
④总时间 t=t1+t2 ⑤
由①②③④⑤解得:

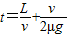
(2)物体在加速阶段与传送带的相对位移
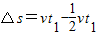 ⑥
⑥发热量Q=μmg△s ⑦
由①②⑥⑦解得

(3)当x≤S1时,物体一直加速,到B的速度为v1,则v12=2μgx
又
 mv12=mgh
mv12=mgh∴h=
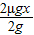 =μx
=μx当x>S1时,物体先加速后匀速,到达B时速度均为v
 mv2=mgh
mv2=mghh′=
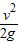
如图所示

答:(1)若物体无初速度放上皮带的右端A处,则其运动到左端B处所需的时间为
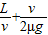 ;
;(2)若物体无初速度放上皮带的右端A处,则其运动到左端B处过程中所产生的热量为
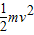 ;
;(3)如图所示.
点评:解决本题的关键根据物块的受力,判断物体的运动状况,加速度是联系前后的桥梁.

练习册系列答案
相关题目
 如图所示的传动装置中,在两轮上分别有A、B两点,已知它们离开转轴的距离分别为OA=R,O'B=2R,利用皮带传动后,两轮一起做匀速转动.则A、B两点的角速度之比为
如图所示的传动装置中,在两轮上分别有A、B两点,已知它们离开转轴的距离分别为OA=R,O'B=2R,利用皮带传动后,两轮一起做匀速转动.则A、B两点的角速度之比为 如图所示,轮半径r=10cm的传送带,水平部分AB的长度L=1.5m,与一圆心在O点半径R=1m的竖直光滑圆轨道的末端相切于A点,AB高出水平地面H=1.25m.一质量m=0.1kg的小滑块(可视为质点),在水平力F作用下静止于圆轨道上的P点,OP与竖直线的夹角θ=37°.已知sin37°=0.6,cos37°=0.8,g=10m/s2,滑块与传送带的动摩擦因数μ=0.1.
如图所示,轮半径r=10cm的传送带,水平部分AB的长度L=1.5m,与一圆心在O点半径R=1m的竖直光滑圆轨道的末端相切于A点,AB高出水平地面H=1.25m.一质量m=0.1kg的小滑块(可视为质点),在水平力F作用下静止于圆轨道上的P点,OP与竖直线的夹角θ=37°.已知sin37°=0.6,cos37°=0.8,g=10m/s2,滑块与传送带的动摩擦因数μ=0.1. 是大轮半径
是大轮半径 的一半,大轮上c点到轮心O'的距离恰等于
的一半,大轮上c点到轮心O'的距离恰等于
 是大轮半径
是大轮半径 的一半,大轮上c点到轮心O'的距离恰等于
的一半,大轮上c点到轮心O'的距离恰等于
