题目内容
9.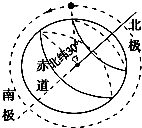 极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,引力常量为G,由以上条件可知( )
极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,引力常量为G,由以上条件可知( )| A. | 地球的质量为$\frac{gR}{G}$ | |
| B. | 卫星运行的线速度为$\frac{πR}{2t}$ | |
| C. | 卫星运行的角速度为$\frac{π}{2t}$ | |
| D. | 卫星距地面的高度为($\frac{4g{R}^{2}{t}^{2}}{{π}^{2}}$)${\;}^{\frac{1}{3}}$ |
分析 地球表面重力等于万有引力,卫星运动的向心力由地球对卫星的万有引力提供,据此展开讨论即可.
解答 解:A、在地球表面上,重力等于万有引力,则得
$\frac{GMm}{{R}^{2}}$=mg,
则得地球的质量为 M=$\frac{{gR}^{2}}{G}$,故A错误;
B、从北纬30°的正上方按图示方向第一次运行至南纬60°正上方转过的圆心角为θ=$\frac{π}{2}$,
据ω=$\frac{θ}{t}$=$\frac{π}{2t}$,
由于轨道半径大于R,根据v=ωr得卫星运行的线速度大于$\frac{πR}{2t}$,故B错误,C正确;
D、根据万有引力提供向心力
$\frac{GMm}{{r}^{2}}$=mω2r
r=($\frac{4g{R}^{2}{t}^{2}}{{π}^{2}}$)${\;}^{\frac{1}{3}}$,所以卫星距地面的高度h=($\frac{4g{R}^{2}{t}^{2}}{{π}^{2}}$)${\;}^{\frac{1}{3}}$-R.故D错误;
故选:C.
点评 灵活运动用重力和万有引力相等以及万有引力提供圆周运动的向心力是解决本题的关键.

练习册系列答案
相关题目
17. 如图所示,A、B是质量均为m的两条磁铁,C为木块,水平放置,静止时A对B的弹力为F1,C对B的弹力为F2,则( )
如图所示,A、B是质量均为m的两条磁铁,C为木块,水平放置,静止时A对B的弹力为F1,C对B的弹力为F2,则( )
 如图所示,A、B是质量均为m的两条磁铁,C为木块,水平放置,静止时A对B的弹力为F1,C对B的弹力为F2,则( )
如图所示,A、B是质量均为m的两条磁铁,C为木块,水平放置,静止时A对B的弹力为F1,C对B的弹力为F2,则( )| A. | F1=mg | B. | F1<mg | C. | F2=2mg | D. | F2>2mg |
4. 如图是某静电分选器的原理示意图.质量相等且带等量异种电荷的a、b两种颗粒在漏斗出口处无初速度下落,经过分离电场后落在水平传送带A、B上(颗粒不会触碰分离电场的极板).忽略颗粒间的库仑力,则( )
如图是某静电分选器的原理示意图.质量相等且带等量异种电荷的a、b两种颗粒在漏斗出口处无初速度下落,经过分离电场后落在水平传送带A、B上(颗粒不会触碰分离电场的极板).忽略颗粒间的库仑力,则( )
 如图是某静电分选器的原理示意图.质量相等且带等量异种电荷的a、b两种颗粒在漏斗出口处无初速度下落,经过分离电场后落在水平传送带A、B上(颗粒不会触碰分离电场的极板).忽略颗粒间的库仑力,则( )
如图是某静电分选器的原理示意图.质量相等且带等量异种电荷的a、b两种颗粒在漏斗出口处无初速度下落,经过分离电场后落在水平传送带A、B上(颗粒不会触碰分离电场的极板).忽略颗粒间的库仑力,则( )| A. | 分选过程中,a颗粒的电势能增大、b颗粒的电势能减小 | |
| B. | 分选过程中,a、b两颗粒的电势能都减小 | |
| C. | 分选过程中,颗粒的运动轨迹一定是抛物线 | |
| D. | 离开分选电场时,a、b两颗粒的水平侧移量一定相等 |
 如图所示的电路中,电源电动势E=6V,内阻r=1Ω,R1=R3=2Ω,R2=3Ω,R4=4Ω,若电表是电压表时,其示数为3.07V,若电表是电流表时,其示数为1.5A.
如图所示的电路中,电源电动势E=6V,内阻r=1Ω,R1=R3=2Ω,R2=3Ω,R4=4Ω,若电表是电压表时,其示数为3.07V,若电表是电流表时,其示数为1.5A.

