Question

航天员站在一星球表面处的某高度，沿水平方向抛出一个小球，经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L，若抛出时的初速增大到2倍，则抛出点与落地点之间的距离为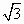L，已知两落地点在同一水平面上，该星球的半径为R，万有引力常数为G，求该星球的质量M．

Answer 1

答案：
解析：

解：设抛出点的高度为h，第一次平抛时的水平射程为x，则有 x2＋h2＝L2　　　　   ① 　 　　由平抛运动规律得知，当初速度增大到原来的2倍，其水平射程也增大到2x，可得： (2x)2＋h2＝(L)2，　　  ② 　 　　由①②可得：　　　　　　　　    h＝L/， 　　设该星球的重力加速度为g，由平抛运动的规律可知 h＝gt2， 　　由万有引力与牛顿第二定律得：G＝mg， 　　式中m为小球的质量，联立以上各式解得：M＝．