题目内容
如图甲所示,一辆货车车厢内紧靠前挡板处有一物体A,其质量m=1×103kg,与车厢间的动摩擦因数μ=0.83.物体A与货车一起以速度v=10m/s,在倾角θ=37°的足够长斜坡上匀速向上行驶.从某时刻货车开始加速运动,v-t图象如图乙所示,物体A与车厢后挡板接触前,已与货车速度相同,此时货车已经做匀速直线运动(空气阻力不计,g取10m/s2,取sin 37°=0.6,cos 37°=0.8).在这个相对滑动过程中,求: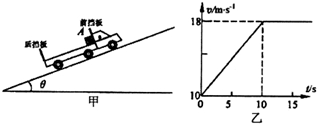
(1)物体A的加速度;
(2)物体A的相对滑动时间;
(3)摩擦力对物体A所做的功.

(1)物体A的加速度;
(2)物体A的相对滑动时间;
(3)摩擦力对物体A所做的功.
分析:(1)设物体A与车厢发生相对滑动时的加速度为a,对A受力分析,由牛顿第二定律即可求解加速度;
(2)根据速度-时间图象可知,物体做匀加速的初速度和末速度,根据v=v0+at即可求解时间.
(3)根据x=v0t+
at2求出A物体的位移,再根据W=μmgcosθ?s求解摩擦力做功.
(2)根据速度-时间图象可知,物体做匀加速的初速度和末速度,根据v=v0+at即可求解时间.
(3)根据x=v0t+
| 1 |
| 2 |
解答:解:
(1)设物体A与车厢发生相对滑动时的加速度为a,对A受力分析,由牛顿第二定律:
μmgcosθ-mgsinθ=ma,
得a=μgcosθ-gsinθ=0.83×10×0.8-10×0.6=0.64m/s2
(2)设物体A与车厢从发生相对滑动到相对静止的时间为t,则
v=v0+at
解得t=
=12.5s
(3)物体A的位移s=v0t+
at2=10×12.5+
×0.64×12.52=175m
摩擦力对物体做的功W=μmgcosθ?s=0.83×10×1000×175×0.8=1.2×106J
答:(1)物体A的加速度为0.64m/s2;
(2)物体A的相对滑动时间为12.5s;
(3)摩擦力对物体A所做的功为1.2×106J.
(1)设物体A与车厢发生相对滑动时的加速度为a,对A受力分析,由牛顿第二定律:
μmgcosθ-mgsinθ=ma,
得a=μgcosθ-gsinθ=0.83×10×0.8-10×0.6=0.64m/s2
(2)设物体A与车厢从发生相对滑动到相对静止的时间为t,则
v=v0+at
解得t=
| 18-10 |
| 0.64 |
(3)物体A的位移s=v0t+
| 1 |
| 2 |
| 1 |
| 2 |
摩擦力对物体做的功W=μmgcosθ?s=0.83×10×1000×175×0.8=1.2×106J
答:(1)物体A的加速度为0.64m/s2;
(2)物体A的相对滑动时间为12.5s;
(3)摩擦力对物体A所做的功为1.2×106J.
点评:解答本题首先要明确物体和车的运动情况,结合图象的物理意义,求解相关的位移,其次关键是寻找两者位移之间的关系.

练习册系列答案
相关题目








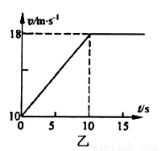
 (3)摩擦力对物体A所做的功。
(3)摩擦力对物体A所做的功。
