题目内容
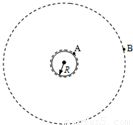
已知地球质量为M，半径为R，自转周期为T，引力常量为G．如图所示，A为在地面附近绕地球做匀速圆周运动的卫星，B为地球的同步卫星．（1）求卫星A运动的速度大小v；
（2）求卫星B到地面的高度h．
【答案】分析：（1）由万有引力充当向心力可得出线速度的大小；
（2）地球同步卫星的周期与地球自转周期相同，则由万有引力充当向心力可求得其离地高度．
解答：解：（1）对卫星A，由牛顿第二定律和万有引力充当向心力可得出
=mA
解得：v=
（2）对卫星B，设它到地面高度为h，同理由万有引力充当向心力可得
G
=m
（R+h）
解得：h=
-R
答：（1）求卫星A运动的速度大小是
；
（2）求卫星B到地面的高度是
-R．
点评：人造地球卫星所受到的万有引力充当向心力，故由向心力公式可求得线速度、角速度、周期等．
（2）地球同步卫星的周期与地球自转周期相同，则由万有引力充当向心力可求得其离地高度．
解答：解：（1）对卫星A，由牛顿第二定律和万有引力充当向心力可得出
=mA解得：v=
（2）对卫星B，设它到地面高度为h，同理由万有引力充当向心力可得
G
=m（R+h）解得：h=
-R答：（1）求卫星A运动的速度大小是
；（2）求卫星B到地面的高度是
-R．点评：人造地球卫星所受到的万有引力充当向心力，故由向心力公式可求得线速度、角速度、周期等．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
（2009?佛山三模）新华社北京10月24日电，24日18时29分，星箭成功分离之后，嫦娥一号卫星进入半径为205公里的圆轨道上绕地球做圆周运动，卫星在这个轨道上“奔跑”一圈半后，于25日下午进行第一次变轨，变轨后，卫星轨道半径将抬高到离地球约600公里的地方．已知地球半径为R，表面重力加速度为g，质量为m的嫦娥一号卫星在地球上空的万有引力势能为Ep=
（以无穷远处引力势能为零）,r表示物体到地心的距离．
（以无穷远处引力势能为零）,r表示物体到地心的距离．