题目内容
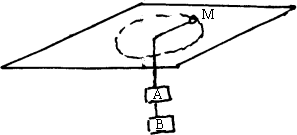
 有一光滑水平板,板的中央有一个小孔,孔内穿入一根光滑轻线,轻线的上端系一质量为M的小球,轻线的下端系着质量分别为m1和m2的两个物体,当小球在光滑水平板上沿半径为R的轨道做匀速率圆周运动时,轻线下端的两个物体都处于静止状态.若将两物体之间的轻线剪断,则小球的线速度为多大时才能再次在水平板上做匀速率圆周运动?
有一光滑水平板,板的中央有一个小孔,孔内穿入一根光滑轻线,轻线的上端系一质量为M的小球,轻线的下端系着质量分别为m1和m2的两个物体,当小球在光滑水平板上沿半径为R的轨道做匀速率圆周运动时,轻线下端的两个物体都处于静止状态.若将两物体之间的轻线剪断,则小球的线速度为多大时才能再次在水平板上做匀速率圆周运动?分析:小球在光滑水平面上做匀速圆周运动,由细线的拉力提供向心力,而轻线下端的物体处于静止状态,合力为零,在将两物体之间的轻线剪断之后,系统的机械能守恒,根据牛顿第二定律、平衡条件和机械能守恒定律求解.
解答: 解:解法一:选小球为研究对象,设小球沿半径为R的轨道做匀速率圆周运动时的线速度为v0,根据牛顿第二定律有:
解:解法一:选小球为研究对象,设小球沿半径为R的轨道做匀速率圆周运动时的线速度为v0,根据牛顿第二定律有:
(m1+m2)g=M
… ①
当剪断两物体之间的轻线后,轻线对小球的拉力减小,不足以维持小球在半径为R的轨道上继续做匀速率圆周运动,于是小球沿切线方向逐渐偏离原来的轨道,同时轻线下端的物体m1逐渐上升,且小球的线速度逐渐减小.
假设物体m1上升高度为h,小球的线速度减为v时,小球在半径为(R+h)的轨道上再次做匀速率圆周运动,根据牛顿第二定律有:
m1g=M
…②
再选小球M、物体m1与地球所组的系统为研究对象,研究两物体间的轻线剪断后物体m1上升的过程,由于只有重力做功,所以系统的机械能守恒.选小球做匀速率圆周运动的水平面为零势面,设小球沿半径为R的轨道做匀速率圆周运动时物体m1到水平板的距离为H,根据机械能守恒定律有:
M
-m1gH=
Mv2-m1g(H-h)…③
以上①②③三式联立解得:v=
.
解法二:与解法一相同,首先列出①②两式,然后再选小球、物体m1与地球组成的系统为研究对象,研究两物体间的轻线剪断后物体m1上升的过程,由于系统的机械能守恒,所以小球M动能的减少量等于物体m1重力势能的增加量.即:
M
-
Mv2=m1gh…④
①②④式联立解得:v=
.
答:小球的线速度为
时才能再次在水平板上做匀速率圆周运动.
 解:解法一:选小球为研究对象,设小球沿半径为R的轨道做匀速率圆周运动时的线速度为v0,根据牛顿第二定律有:
解:解法一:选小球为研究对象,设小球沿半径为R的轨道做匀速率圆周运动时的线速度为v0,根据牛顿第二定律有:(m1+m2)g=M
| ||
| R |
当剪断两物体之间的轻线后,轻线对小球的拉力减小,不足以维持小球在半径为R的轨道上继续做匀速率圆周运动,于是小球沿切线方向逐渐偏离原来的轨道,同时轻线下端的物体m1逐渐上升,且小球的线速度逐渐减小.
假设物体m1上升高度为h,小球的线速度减为v时,小球在半径为(R+h)的轨道上再次做匀速率圆周运动,根据牛顿第二定律有:
m1g=M
| v2 |
| R+h |
再选小球M、物体m1与地球所组的系统为研究对象,研究两物体间的轻线剪断后物体m1上升的过程,由于只有重力做功,所以系统的机械能守恒.选小球做匀速率圆周运动的水平面为零势面,设小球沿半径为R的轨道做匀速率圆周运动时物体m1到水平板的距离为H,根据机械能守恒定律有:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
以上①②③三式联立解得:v=
|
解法二:与解法一相同,首先列出①②两式,然后再选小球、物体m1与地球组成的系统为研究对象,研究两物体间的轻线剪断后物体m1上升的过程,由于系统的机械能守恒,所以小球M动能的减少量等于物体m1重力势能的增加量.即:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
①②④式联立解得:v=
|
答:小球的线速度为
|
点评:解决本题的关键知道圆周运动向心力的来源和系统的机械能守恒,知道稳定时细线拉力等于下端物体的重力.

练习册系列答案
相关题目