题目内容
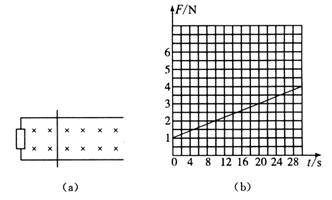
如图（a）所示，一平行光滑轨道放置在水平面上，两轨道间距L=0.2m，电阻R=1.0Ω。有一导体杆静止地放在轨道上，杆与轨道的电阻皆可忽略不计，整个装置处于磁感应强度为B=0.50T的匀强磁场中，磁场的方向垂直于轨道面向下。现用一外力拉导体杆，使导体做加速度为a的匀加速运动，F与时间t的关系如图（b）所示，求杆的质量m和加速度a.
【答案】
a=10m/s2 m=0.1kg
【解析】
试题分析：分析其受力：水平方向上，安培力和外力F，由题意导体杆匀加速运动，所以合外力恒定，即F-F安=ma；根据法拉第电磁感应定律求出安培力的表达式，再结合图形即可解题：
导体杆与光滑轨道、电阻R组成闭合回路，当杆向右运动时在回路中产生感应电流，杆在外力和安培力作用下匀加速运动，经时间t速度为υ，则有：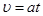
杆切割磁感线，产生感应电动势，由法拉第电磁感应定律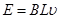
由右手定则判断感应电流方向为逆时针方向，根据欧姆定律：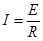
杆受到的安培力，由楞次定律中的阻碍知：方向向左，大小为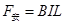
根据牛顿第二定律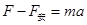
解以上各式得：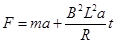
，这就是外力F和时间t的函数关系。
在图像上任意取两点即可解得结果，
如取（0，1）和（20，3）两点代入最后的函数关系就能得两个方程，
解得：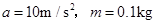
考点：考查法拉第电磁感应定律、欧姆定律、牛顿第二定律的应用
点评: 本题是一道电磁感应与力学知识相结合的问题，综合性较强，涉及到力和运动.导体杆向右运动时切割磁感线，回路中产生感应电流
练习册系列答案
阅读快车系列答案
相关题目
（2011?徐汇区模拟）如图（a）所示，轻质T型支架与地面铰接于O点，支架左端A搁置在一小平台上，AB保持水平，AP=PB=2m；在AP中点悬挂一质量为M=4.2kg的重物．一个质量为m=4kg的木块在水平拉力F=10N作用下从A点由静止开始向右运动．当木块运动至P处时，改变拉力F的方向但不改变拉力F的大小，直至离开A点某距离处支架翻转．已知木块与T型支架之间的动摩擦因素为μ=0.2．木块水平运动过程中对支架摩擦力关于O点的力矩大小Mf随离开A点位移x的关系图如图（b）所示．求：（g=10m/s2）
