题目内容
14.如图,高h、长L的光滑绝缘正方形台面上加有一竖直向下、磁感应强度B的匀强磁场.在台面右侧接着一个与内侧边线对齐、每板宽为d(<$\frac{L}{2}$)的平行板电容器(电容器有光滑绝缘的底部),右板接电源的正极,左板接电源负极,现有质量为m、电量为+q的一群粒子(视为质点)从靠近右板在底部由静止释放,通过左板的小孔进入磁场,不计一切阻力,重力加速度取g.
(1)若取电容器的电压为U,求这些带电粒子在磁场中运动的半径;
(2)若要求这些粒子都从台面右侧射出,则电容器的电压应满足什么条件?
(3)在地面建立如图坐标系,当U=$\frac{q{B}^{2}{L}^{2}}{32m}$时,画出这些粒子落地时在这个坐标系中的PQ连线.
分析 (1)由动能定理可求得带电粒子离开电容器时的速度,再由洛仑力充当向心力可求得粒子在磁场中的半径;
(2)由几何关系可得出最大半径,则可求出最大电压,分析粒子的运动可得出电压的范围;
(3)由已知电压可得出粒子在磁场中的半径,分析粒子到这位置,再根据电场中的类平抛运动规律可求得粒了偏转的位移.
解答 解:(1)在电容器中,根据动能定理,有:$qU=\frac{1}{2}m{v}^{2}$ ①
在磁场中,根据洛仑兹力等于向心力,有:$qvB=m\frac{{v}^{2}}{R}$ ②
①②联立得粒子运动的半径为:$R=\sqrt{\frac{2mU}{q{B}^{2}}}$ ③
(2)当在电容器底部外侧经加速的粒子恰好能从台面的外侧相切射出时,粒子的半径最大,如图所示.
即${R}_{m}=\frac{L-d}{2}$ ④
④代入③解得:${U}_{m}=\frac{(L-d)^{2}q{B}^{2}}{8m}$ ⑤
当U>0,在电容器内侧粒子,那怕不能一次在磁场中从台面右侧射出,也可以再进入电容器减速至底部右侧,又再重新加速进入磁场,多周后也能从台面右侧射出.
故电容器的电压满足的条件为:$0<{U}_{m}≤\frac{(L-d)^{2}q{B}^{2}}{8m}$.
(3)把$U=\frac{q{B}^{2}{L}^{2}}{32m}$代入③得粒子运动的半径为:$R=\frac{L}{4}$.
说明当粒子从电容器远侧射入磁场时,粒子从台面右侧中点射出,当粒子从电容器近侧射入磁场时,粒子从台面距中点为d处射出.
粒子从台面右侧射出后做平抛运动,设它的落地时间为t.
由$h=\frac{1}{2}g{t}^{2}$,得:$t=\sqrt{\frac{2h}{g}}$,
粒子水平位移x=vt=$\frac{qBL}{4m}\sqrt{\frac{2h}{g}}$.
至此可作得这些粒子落地时的轨迹如右图所示中的PQ连线.
答:(1)这些带电粒子在磁场中运动的半径为$\sqrt{\frac{2mU}{q{B}^{2}}}$;
(2)电容器的电压应满足:$0<{U}_{m}≤\frac{(L-d)^{2}q{B}^{2}}{8m}$.
(3)这些粒子落地时的轨迹如右图所示中的PQ连线.
点评 本题为带电粒子磁场及电场中的运动问题,要注意全面掌握粒子的运动情况,明确几何关系及运动的合成与分解在解题中的应用.

 如图甲所示,a、b两条直导线垂直于纸面水平放置,且通有的电流大小相等,方向如图所示,图乙中c、d是两个电荷量相等的正点电荷,O1和O2分别为两直导线和两点电荷连线的中点,在O1和O2正上方均有一电子,以较小的速度v竖直向下射出,不计电子重力.则电子( )
如图甲所示,a、b两条直导线垂直于纸面水平放置,且通有的电流大小相等,方向如图所示,图乙中c、d是两个电荷量相等的正点电荷,O1和O2分别为两直导线和两点电荷连线的中点,在O1和O2正上方均有一电子,以较小的速度v竖直向下射出,不计电子重力.则电子( )| A. | 在乙图中将做往复运动 | |
| B. | 在甲图中将做匀加速直线运动 | |
| C. | 在乙图中向O2点运动时,加速度一定减小 | |
| D. | 在乙图中到达O2点时动能最小,电势能最大 |
 如图所示,水平转台上放着一枚硬币,当转台匀速转动时,硬币没有滑动.关于这种情况下硬币的受力情况,下列说法中正确的是( )
如图所示,水平转台上放着一枚硬币,当转台匀速转动时,硬币没有滑动.关于这种情况下硬币的受力情况,下列说法中正确的是( )| A. | 仅受重力和台面的支持力 | |
| B. | 受重力、台面的支持力、静摩擦力和向心力 | |
| C. | 受重力、台面的支持力、沿切线与速度方向相反的静摩擦力 | |
| D. | 受重力、台面的支持力、指向圆心的静摩擦力 |
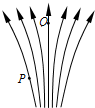
| A. | P点电势高于Q点电势 | |
| B. | P、Q两点场强大小相等、方向相同 | |
| C. | 同一正电荷分别置于P、Q两点时电势能相等 | |
| D. | 同一负电荷从P点移至Q点,电场力做负功,电势能增大 |
 如图所示,光滑水平面上有大小相同的两个A、B小球在同一直线上运动.两球质量关系为mB=2mA,规定向右为正方向,A、B两球的动量均为8kgm/s运动中两球发生碰撞,碰撞后A球的动量增量为-4kgm/s,则( )
如图所示,光滑水平面上有大小相同的两个A、B小球在同一直线上运动.两球质量关系为mB=2mA,规定向右为正方向,A、B两球的动量均为8kgm/s运动中两球发生碰撞,碰撞后A球的动量增量为-4kgm/s,则( )| A. | 右方为A球,碰撞后A、B两球的速度大小之比为2:3 | |
| B. | 右方为A球,碰撞后A、B两球的速度大小之比为1:6 | |
| C. | 左方为A球,碰撞后A、B两球的速度大小之比为2:3 | |
| D. | 左方为A球,碰撞后A、B两球的速度大小之比为1:6 |
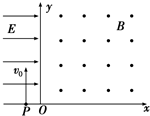 如图所示,在第二象限中有水平向右的匀强电场,电场强度为E,在第一象限内存在垂直纸面向外的匀强磁场,磁感应强度大小为B.有一重力不计的带电粒子以垂直于x轴的速度v0=10m/s从x轴上的P点进入匀强电场,恰好与y轴成45°角射出电场,再经过一段时间又恰好垂直于x轴进入第四象限.已知OP之间的距离为d=0.5m,则带电粒子( )
如图所示,在第二象限中有水平向右的匀强电场,电场强度为E,在第一象限内存在垂直纸面向外的匀强磁场,磁感应强度大小为B.有一重力不计的带电粒子以垂直于x轴的速度v0=10m/s从x轴上的P点进入匀强电场,恰好与y轴成45°角射出电场,再经过一段时间又恰好垂直于x轴进入第四象限.已知OP之间的距离为d=0.5m,则带电粒子( )| A. | 带正电荷 | B. | 在电场中运动的时间为0.1s | ||
| C. | 在磁场中做圆周运动的半径为$\frac{\sqrt{2}}{2}$m | D. | 在磁场中运动的时间为$\frac{3π}{40}$s |
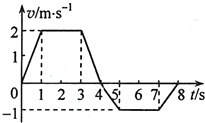 一质点沿x轴做直线运动,其V-t图象如图所示.质点在v=0时位于x=5m处,开始沿x轴正向运动.当t=8s时,质点在轴上的位置为( )
一质点沿x轴做直线运动,其V-t图象如图所示.质点在v=0时位于x=5m处,开始沿x轴正向运动.当t=8s时,质点在轴上的位置为( )| A. | x=3m | B. | x=8m | C. | x=9m | D. | x=-14m |

| A. | 该金属的逸出功等于hv0 | |
| B. | 遏止电压是确定的,与照射光的频率无关 | |
| C. | 若已知电子电量e,就可以求出普朗克常量h | |
| D. | 入射光的频率为2v0时,产生的光电子的最大初动能为hv0 |
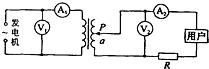 如图所示,理想变压器原线圈匝数 n1=140匝,副线圈总匝数 n2=1400匝,原线圈电压μ1=10V,线路电阻用R表示,R=4,用户电阻R′=16Ω.开始时滑动触头P放在副线圈的中点,不计电表对电路的影响,求:
如图所示,理想变压器原线圈匝数 n1=140匝,副线圈总匝数 n2=1400匝,原线圈电压μ1=10V,线路电阻用R表示,R=4,用户电阻R′=16Ω.开始时滑动触头P放在副线圈的中点,不计电表对电路的影响,求: