题目内容
14.汽车沿平直公路由静止开始做匀加速直线运动,经50S,速度由5m/s增加至15m/s,若汽车质量为104kg,在运动中受到阻力为车重的0.05倍,取g=10m/s2,求:(1)汽车发动机的平均功率;
(2)在这段运动的时间中点发动机的瞬时功率.
分析 (1)根据加速度定义求解加速度,根据牛顿运动定律求解牵引力,根据平均功率P=F$\overline{v}$求解功率;
(2)瞬时功率P=Fv${\;}_{\frac{t}{2}}$求解瞬时功率.
解答 解:(1)经50S,速度由5m/s增加至15m/s
则加速度a=$\frac{v-{v}_{0}}{t}$=$\frac{15-5}{50}$m/s2=0.2m/s2
根据牛顿运动定律知F=ma+f=104×0.2+105×0.05=7×103N
平均功率P=F$\overline{v}$=F•$\frac{{v}_{0}+v}{2}$=7×103$•\frac{5+15}{2}$=7×104W
(2)在这段运动的时间中点发动机的瞬时功率P=Fv${\;}_{\frac{t}{2}}$=F•$\frac{{v}_{0}+v}{2}$=7×103$•\frac{5+15}{2}$=7×104W
答:(1)汽车发动机的平均功率为7×104W;
(2)在这段运动的时间中点发动机的瞬时功率为7×104W.
点评 本题关键是明确匀加速启动牵引力恒定,知道匀变速直线运动$\overline{v}$=v${\;}_{\frac{t}{2}}$=$\frac{{v}_{0}+v}{2}$.会应用P=Fv,平均功率速度为平均速度,瞬时功率速度为瞬时速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图所示,在水平方向的匀强电场中,绝缘细线的一端固定在O点,另一端系一带正电的小球在竖直平面内做圆周运动,小球所受的电场力大小等于重力大小,比较a、b、c、d这四点,该小球( )
如图所示,在水平方向的匀强电场中,绝缘细线的一端固定在O点,另一端系一带正电的小球在竖直平面内做圆周运动,小球所受的电场力大小等于重力大小,比较a、b、c、d这四点,该小球( )
 如图所示,在水平方向的匀强电场中,绝缘细线的一端固定在O点,另一端系一带正电的小球在竖直平面内做圆周运动,小球所受的电场力大小等于重力大小,比较a、b、c、d这四点,该小球( )
如图所示,在水平方向的匀强电场中,绝缘细线的一端固定在O点,另一端系一带正电的小球在竖直平面内做圆周运动,小球所受的电场力大小等于重力大小,比较a、b、c、d这四点,该小球( )| A. | 在a处电势能最小 | B. | 在c处重力势能最小 | ||
| C. | 在水平直径右端b处机械能最大 | D. | 在水平直径左端d处总能量最大 |
19.在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.为了能较准确地描绘运动轨迹,下面的操作,不正确的是( )
| A. | 通过调节使斜槽的末端保持水平 | |
| B. | 保证每次释放小球的位置相同 | |
| C. | 小球运动时不应与木板上的白纸(或方格纸)相接触 | |
| D. | 将球的位置记录在纸上后,取下纸,用直尺将点连成折线 |
6. 如图所示,物体的运动分三段,第1、2s为第Ⅰ段,第3、4s为第Ⅱ段,第5s为第Ⅲ段,则下列说法正确的是( )
如图所示,物体的运动分三段,第1、2s为第Ⅰ段,第3、4s为第Ⅱ段,第5s为第Ⅲ段,则下列说法正确的是( )
 如图所示,物体的运动分三段,第1、2s为第Ⅰ段,第3、4s为第Ⅱ段,第5s为第Ⅲ段,则下列说法正确的是( )
如图所示,物体的运动分三段,第1、2s为第Ⅰ段,第3、4s为第Ⅱ段,第5s为第Ⅲ段,则下列说法正确的是( )| A. | 第1s内与第5s内的速度方向相反 | B. | 第1s的加速度大于第5s的加速度 | ||
| C. | 第I段与第III段的平均速度相等 | D. | 第I段与第III段的位移之比为1:2 |
3. 如图所示,作用于O点的三个力平衡,设其中一个力大小为F1,沿-y方向,大小未知的力F2与+x方向夹角为θ,下列说法正确的是( )
如图所示,作用于O点的三个力平衡,设其中一个力大小为F1,沿-y方向,大小未知的力F2与+x方向夹角为θ,下列说法正确的是( )
 如图所示,作用于O点的三个力平衡,设其中一个力大小为F1,沿-y方向,大小未知的力F2与+x方向夹角为θ,下列说法正确的是( )
如图所示,作用于O点的三个力平衡,设其中一个力大小为F1,沿-y方向,大小未知的力F2与+x方向夹角为θ,下列说法正确的是( )| A. | 力F3只能在第二象限 | |
| B. | 力F3只能在第三象限 | |
| C. | 力F3与F2的夹角越小,则F3与F2的合力越小 | |
| D. | F3的最小值为F1cosθ |
4.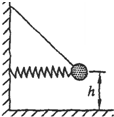 用细绳拴一个质量为m的小球,小球将固定在墙上的轻弹簧水平压缩的距离为x,球离地高h,球与弹簧不粘连,如图所示,将细线烧断后( )
用细绳拴一个质量为m的小球,小球将固定在墙上的轻弹簧水平压缩的距离为x,球离地高h,球与弹簧不粘连,如图所示,将细线烧断后( )
 用细绳拴一个质量为m的小球,小球将固定在墙上的轻弹簧水平压缩的距离为x,球离地高h,球与弹簧不粘连,如图所示,将细线烧断后( )
用细绳拴一个质量为m的小球,小球将固定在墙上的轻弹簧水平压缩的距离为x,球离地高h,球与弹簧不粘连,如图所示,将细线烧断后( )| A. | 小球做平抛运动 | B. | 小球的加速度立即为g | ||
| C. | 小球脱离弹簧后做匀变速运动 | D. | 小球落地时动能大于mgh |
 如图所示是研究平抛运动的实验装置简图,图是实验后白纸上的轨迹图.
如图所示是研究平抛运动的实验装置简图,图是实验后白纸上的轨迹图.
